Este é um vector:

Um vector tem magnitude (tamanho) e direcção:

O comprimento da linha mostra a sua magnitude e a ponta da seta aponta na direcção.
Podemos adicionar dois vectores juntando-os frente a frente:
E não importa a ordem em que os adicionamos, obtemos o mesmo resultado:
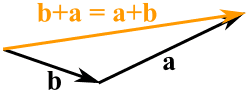
Exemplo: Um avião está a voar, apontando para Norte, mas há um vento que vem do Noroeste.
Os dois vectores (a velocidade causada pela hélice, e a velocidade do vento) resultam numa velocidade no solo ligeiramente mais lenta dirigindo-se um pouco para Este do Norte.
Se observasse o avião a partir do solo parece estar a deslizar um pouco para os lados.
Viu alguma vez isso acontecer? Talvez já tenha visto aves a lutar contra um vento forte que parecem voar de lado. Os vectores ajudam a explicar que.
Velocidade, aceleração, força e muitas outras coisas são vectores.
Subtrair
p>Podemos também subtrair um vector de outro:
- primeiro invertemos a direcção do vector que queremos subtrair,
- depois adicionamo-los como habitualmente:
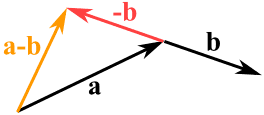
a – b
Notação
Um vector é frequentemente escrito em negrito, como a ou b.
| Um vector também pode ser escrito como as letras da sua cabeça e cauda com uma seta por cima, desta forma: |
 |
Cálculos
Now …. como é que fazemos os cálculos?
A forma mais comum é primeiro dividir os vectores em partes de x e y, como isto:
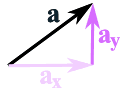
O vector a é dividido em
os dois eixos vectoriais e ay
(Vemos mais tarde como fazer isto.)
Adicionando Vectores
Podemos então adicionar vectores adicionando as partes x e adicionando as partes y:
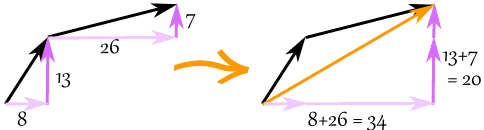 vector add example
vector add example
O vector (8, 13) e o vector (26, 7) adicionam-se ao vector (34, 20)
Exemplo: adicionar os vectores a = (8, 13) e b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Quando quebramos um vector assim, cada parte é chamada componente:
Subtrair Vectores
Para subtrair, primeiro inverter o vector que queremos subtrair, depois adicionar.
Exemplo: subtrair k = (4, 5) de v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitude de um Vector
A magnitude de um vector é mostrada por duas barras verticais em cada lado do vector:
|a|
OR pode ser escrito com barras verticais duplas (de modo a não confundir com valor absoluto):
|||||a|||
Usamos o teorema de Pitágoras para o calcular:
|a| = √( x2 + y2 )
Exemplo: qual é a magnitude do vector b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Um vector com magnitude 1 é chamado Unit Vector.
Vector vs Scalar
Um escalar tem apenas magnitude (tamanho).
Scalar: apenas um número (como 7 ou -0,32) …. definitivamente não é um vector.
Um vector tem magnitude e direcção, e é frequentemente escrito em negrito, por isso sabemos que não é um escalar:
- sim c é um vector, tem magnitude e direcção
- mas c é apenas um valor, como 3 ou 12.4
Exemplo: kb é na realidade o escalar k vezes o vector b.
Multiplicando um Vector por um Scalar
Quando multiplicamos um vector por um escalar chama-se “escalar” um vector, porque mudamos o quão grande ou pequeno é o vector.
Exemplo: multiplicar o vector m = (7, 3) pelo escalar 3
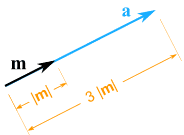 |
a = 3m = (3×7, 3×3) = (21, 9) |
Ainda aponta na mesma direcção, mas é 3 vezes mais longo
(E agora sabe porque é que os números são chamados “escalares”, porque “escalam” o vector para cima ou para baixo.)
Multiplicando um Vector por um Vector (Produto Ponto e Produto Cruzado)
 |
Como multiplicamos dois vectores em conjunto? Há mais de uma forma!
(Leia estas páginas para mais detalhes.) |
Mais de 2 Dimensões
Vectores também funcionam perfeitamente bem em 3 ou mais dimensões:

Exemplo: adicionar os vectores a = (3, 7, 4) e b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Exemplo: qual é a magnitude do vector w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Aqui está um exemplo com 4 dimensões (mas é difícil de desenhar!):
Exemplo: subtrair (1, 2, 3, 4) de (3, 3, 3, 3, 3)
(3, 3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Magnitude e Direcção
Podemos conhecer a magnitude e direcção de um vector, mas queremos os seus comprimentos x e y (ou vice versa):
 |
<> |  |
| Vector a em Polar Coordenadas |
Vector a em cartesiano Coordenadas |
P>Pode ler como convertê-las em coordenadas polares e cartesianas, mas aqui está um breve resumo:
| de coordenadas polares (r,θ) para coordenadas cartesianas (x,y) |
de coordenadas cartesianas (x,y) para coordenadas polares (r,θ) |
|
|---|---|---|
|
|
Um exemplo
Sam e Alex estão a puxar uma caixa.
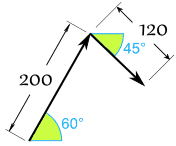
- Sam puxa com 200 Newtons de força a 60°
- Alex puxa com 120 Newtons de força a 45° como mostrado
Qual é a força combinada, e a sua direcção?
Deixe-nos adicionar os dois vectores cabeça à cauda:
P>Primeiro converter de polar para cartesiano (até 2 decimais):
p>Vector da Sam:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0,8660 = 173.21
Alex’s Vector:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0,7071 = 84,85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84,85
- r = √ ( x2 + y2 ) = √ ( 184,852 + 88,362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88,36 / 184,85 ) = 25.5°
Agora temos:
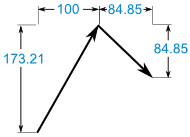
Adicioná-los:
(100, 173,21) + (84,85, -84,85) = (184.85, 88,36)
Essa resposta é válida, mas voltemos a converter para polar como a pergunta estava em polar:
E temos este resultado (arredondado):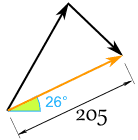
E parece assim para Sam e Alex:
p>p>Poderiam obter um resultado melhor se estivessem ombro a ombro!



