p>Teoria Gráfica >
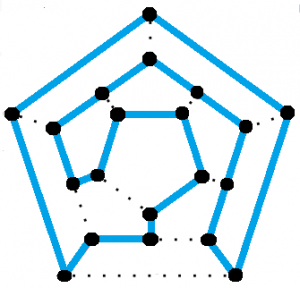
Um dodecaedro (uma figura sólida regular com doze faces pentagonais iguais) tem um ciclo hamiltoniano.
Um ciclo Hamiltoniano é um ciclo fechado num gráfico onde cada nó (vértice) é visitado exactamente uma vez.
Um ciclo Hamiltoniano é apenas uma borda que une um nó a si próprio; assim, um ciclo Hamiltoniano é um caminho que viaja de um ponto de volta a si próprio, visitando cada nó no caminho.
Se um gráfico com mais de um nó (isto é, um gráfico não unívoco) tem este tipo de ciclo, chamamos-lhe um gráfico hamiltoniano.
Não há nenhuma equação ou truque geral para descobrir se um gráfico tem um ciclo hamiltoniano; a única maneira de determinar isto é fazer uma pesquisa completa e exaustiva, passando por todas as opções.
História do ciclo Hamiltoniano
O ciclo recebeu o nome de Sir William Rowan Hamilton que, em 1857, inventou um jogo de puzzle que envolvia a caça a um ciclo Hamiltoniano. O jogo, chamado jogo Icosiano, foi distribuído como um gráfico de dodecaedro com um buraco em cada vértice. Para resolver o puzzle ou ganhar o jogo era preciso usar cavilhas e cordel para encontrar o ciclo Hamiltoniano – um circuito fechado que visitava cada buraco exactamente uma vez. A solução é mostrada na imagem acima.
Exemplos de Gráficos Hamiltonianos
Um gráfico Hamiltoniano completo com mais de dois vértices é um gráfico Hamiltoniano. Isto decorre da definição de um gráfico completo: um gráfico não dirigido e simples de tal forma que cada par de nós está ligado por uma borda única.
O gráfico de cada sólido platónico é um gráfico hamiltoniano. Assim, o gráfico de um cubo, um tetraedro, um octaedro, ou um icosaedro são todos gráficos hamiltonianos com ciclos hamiltonianos.
Um gráfico com n vértices (onde n > 3) é hamiltoniano se a soma dos graus de cada par de vértices não adjacentes for n ou maior. Isto é conhecido como teorema de Ore.
Aplicações dos ciclos e gráficos Hamiltonianos
Uma pesquisa destes ciclos não é apenas um jogo divertido para a tarde de folga. Tem aplicações reais em campos tão diversos como computação gráfica, desenho de circuitos electrónicos, mapeamento de genomas, e pesquisa de operações.
Por exemplo, quando mapeiam genomas os cientistas devem combinar muitos pequenos fragmentos de código genético (“lê”, são chamados), numa única sequência genómica (uma “supercorda”). Isto pode ser feito encontrando um caminho ou ciclo Hamiltoniano, onde cada uma das leituras é considerada como um nó num gráfico e cada sobreposição (local onde o fim de uma leitura coincide com o início de outra) é considerada como uma borda.
Numa aplicação muito menos complexa de exactamente a mesma matemática, os distritos escolares usam Hamiltonianos para planear o melhor caminho para apanhar estudantes de todo o distrito. Aqui os estudantes podem ser considerados nós, os caminhos entre eles, e o autocarro deseja percorrer uma rota que passará por cada casa de estudantes exactamente uma vez.
p>Jogo Cosmosiano
Em Ciclos Hamiltonianos e Caminhos Hamiltonianos
Assemblagem de Gênomos
Gráfico Algoritmos em Bioinformáticadiv> CITA ESTE AS:
Stephanie Glen. “Ciclo Hamiltoniano”: Definição Simples e Exemplo” de StatisticsHowTo.com: Estatística elementar para o resto de nós! https://www.statisticshowto.com/hamiltonian-cycle/ ——————————————————————————
p>Need help with a homework or test question? Com o Chegg Study, pode obter soluções passo a passo para as suas perguntas de um especialista na matéria. Os seus primeiros 30 minutos com um tutor do Chegg são gratuitos!