Grafentheorie >

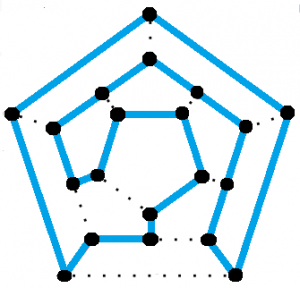
Een dodecaëder (een regelmatig massief figuur met twaalf gelijke vijfhoekige zijvlakken) heeft een Hamiltoniaanse cyclus.

Een Hamiltoniaanse cyclus is een gesloten lus in een grafiek waarin elk knooppunt (hoekpunt) precies één keer wordt bezocht.

Een lus is gewoon een rand die een knooppunt met zichzelf verbindt; een Hamiltoniaanse cyclus is dus een pad dat van een punt terug naar zichzelf loopt, waarbij onderweg elk knooppunt wordt bezocht.

Als een grafiek met meer dan één knoop (dus een niet-singleton grafiek) dit soort cycli heeft, noemen we het een Hamiltoniaanse grafiek.

Er is geen vergelijking of algemene truc om uit te vinden of een grafiek een Hamiltoniaanse cyclus heeft; de enige manier om dit te bepalen is door een volledige en uitputtende zoektocht te doen, waarbij alle mogelijkheden worden doorlopen.

Geschiedenis van de Hamiltoniaanse cyclus

De cyclus is vernoemd naar Sir William Rowan Hamilton, die in 1857 een puzzelspel uitvond waarbij gezocht moest worden naar een Hamiltoniaanse cyclus. Het spel, dat het Icosiaanse spel werd genoemd, was verdeeld als een dodecaëder-grafiek met een gat op elk hoekpunt. Om de puzzel op te lossen of het spel te winnen moest men gebruik maken van knijpers en touw om de Hamiltoniaanse cyclus te vinden – een gesloten lus die elk gat precies één keer bezocht. De oplossing is te zien in de afbeelding hierboven.

Voorbeelden van Hamiltoniaanse grafieken

Elke volledige grafiek met meer dan twee hoekpunten is een Hamiltoniaanse grafiek. Dit volgt uit de definitie van een complete grafiek: een ongerichte, eenvoudige grafiek waarbij elk knooppuntpaar door een unieke rand verbonden is.

De grafiek van elk platonisch vast lichaam is een Hamiltoniaanse grafiek. Dus de grafiek van een kubus, een tetraëder, een octaëder, of een icosaëder zijn allemaal Hamiltoniaanse grafieken met Hamiltoniaanse cycli.

Een grafiek met n hoekpunten (waarbij n > 3) is Hamiltoniaans als de som van de graden van elk paar niet-aangrenzende hoekpunten n of groter is. Dit staat bekend als de stelling van Ore.

Toepassingen van Hamiltoniaanse cycli en grafieken

Het zoeken naar deze cycli is niet alleen een leuk spelletje voor de vrije middag. Het heeft echte toepassingen op zulke uiteenlopende gebieden als computergrafiek, het ontwerpen van elektronische circuits, het in kaart brengen van genomen, en operations research.

Bij het in kaart brengen van genomen moeten wetenschappers bijvoorbeeld vele kleine fragmenten genetische code (“reads”, worden ze genoemd) combineren tot één enkele genomische sequentie (een “superstring”). Dit kan worden gedaan door een Hamiltoniaans pad of cyclus te vinden, waarbij alle gelezen fragmenten als knooppunten in een grafiek worden beschouwd en elke overlap (de plaats waar het einde van een gelezen fragment overeenkomt met het begin van een ander) als een rand wordt beschouwd.

In een veel minder complexe toepassing van precies dezelfde wiskunde, gebruiken schooldistricten Hamiltoniaanse paden om de beste route te plannen voor het ophalen van leerlingen uit het hele district. Hier worden de leerlingen als knooppunten beschouwd, de paden tussen hen als ribben, en de bus wil een route afleggen waarbij hij elk huis van de leerling precies één keer passeert.

Icosiaans spel
Over Hamiltoniaanse cycli en Hamiltoniaanse paden
Genome Assembly
Graph Algorithms in Bioinformatics

——————————————————————————

Heb je hulp nodig bij een huiswerk- of toetsvraag? Met Chegg Study kunt u stap-voor-stap oplossingen voor uw vragen krijgen van een expert op dit gebied. Uw eerste 30 minuten met een Chegg-leraar zijn gratis!