Graphentheorie >

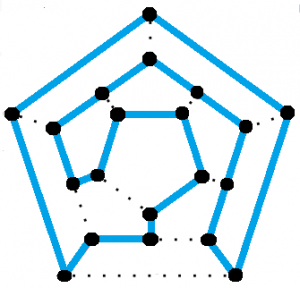
Ein Dodekaeder (eine regelmäßige feste Figur mit zwölf gleichen fünfeckigen Flächen) hat einen Hamiltonschen Zyklus.

Ein Hamilton’scher Zyklus ist eine geschlossene Schleife auf einem Graphen, bei der jeder Knoten (Vertex) genau einmal besucht wird.

Eine Schleife ist nur eine Kante, die einen Knoten mit sich selbst verbindet; ein Hamilton’scher Zyklus ist also ein Pfad, der von einem Punkt zurück zu sich selbst führt und dabei jeden Knoten auf dem Weg besucht.

Wenn ein Graph mit mehr als einem Knoten (d.h. ein Nicht-Singleton-Graph) diese Art von Zyklus hat, nennen wir ihn einen Hamilton-Graphen.

Es gibt keine Gleichung oder einen allgemeinen Trick, um herauszufinden, ob ein Graph einen Hamilton-Zyklus hat; die einzige Möglichkeit, dies zu bestimmen, ist eine vollständige und erschöpfende Suche, die alle Möglichkeiten durchläuft.

Geschichte des Hamiltonschen Zyklus

Der Zyklus wurde nach Sir William Rowan Hamilton benannt, der 1857 ein Rätselspiel erfand, bei dem es um die Suche nach einem Hamiltonschen Zyklus ging. Das Spiel, genannt Ikosianisches Spiel, wurde als Dodekaeder-Graph mit einem Loch an jedem Vertex verteilt. Um das Rätsel zu lösen oder das Spiel zu gewinnen, musste man mit Hilfe von Pflöcken und Schnüren den Hamilton’schen Zyklus finden – eine geschlossene Schleife, die jedes Loch genau einmal besucht. Die Lösung ist im Bild oben zu sehen.

Beispiele für Hamiltonsche Graphen

Jeder vollständige Graph mit mehr als zwei Scheitelpunkten ist ein Hamiltonscher Graph. Dies folgt aus der Definition eines vollständigen Graphen: ein ungerichteter, einfacher Graph, bei dem jedes Knotenpaar durch eine eindeutige Kante verbunden ist.

Der Graph eines jeden platonischen Körpers ist ein Hamiltonscher Graph. So sind der Graph eines Würfels, eines Tetraeders, eines Oktaeders oder eines Ikosaeders alles Hamiltonsche Graphen mit Hamiltonschen Zyklen.

Ein Graph mit n Scheitelpunkten (wobei n > 3) ist Hamiltonsch, wenn die Summe der Grade jedes Paares von nicht benachbarten Scheitelpunkten n oder größer ist. Dies ist als Ore’s Theorem bekannt.

Anwendungen von Hamiltonschen Zyklen und Graphen

Die Suche nach diesen Zyklen ist nicht nur ein lustiges Spiel für den freien Nachmittag. Sie hat reale Anwendungen in so unterschiedlichen Bereichen wie Computergrafik, Entwurf elektronischer Schaltkreise, Kartierung von Genomen und Operations Research.

Beim Kartieren von Genomen müssen Wissenschaftler zum Beispiel viele winzige Fragmente des genetischen Codes („Reads“ genannt) zu einer einzigen genomischen Sequenz (einem „Superstring“) kombinieren. Dies kann durch die Suche nach einem Hamiltonschen Pfad oder Zyklus geschehen, wobei jeder der Reads als Knoten in einem Graphen und jede Überlappung (Ort, an dem das Ende eines Reads mit dem Anfang eines anderen übereinstimmt) als Kante betrachtet wird.

In einer viel weniger komplexen Anwendung genau derselben Mathematik verwenden Schulbezirke Hamiltonianer, um die beste Route zum Abholen von Schülern aus dem ganzen Bezirk zu planen. Hier können die Schüler als Knoten betrachtet werden, die Wege zwischen ihnen als Kanten, und der Bus möchte eine Route fahren, die an jedem Schülerhaus genau einmal vorbeiführt.

Icosian Game
On Hamiltonian Cycles and Hamiltonian Paths
Genome Assembly
Graph Algorithms in Bioinformatics

——————————————————————————

Brauchen Sie Hilfe bei einer Hausaufgabe oder Testfrage? Mit Chegg Study können Sie Schritt-für-Schritt-Lösungen zu Ihren Fragen von einem Experten auf dem Gebiet erhalten. Ihre ersten 30 Minuten mit einem Chegg Tutor sind kostenlos!