Objetivos de aprendizaje

  • Describir el movimiento del movimiento armónico amortiguado
  • Escribir las ecuaciones de movimiento para las oscilaciones armónicas amortiguadas
  • Describir el movimiento del movimiento armónico impulsado, o forzado, movimiento armónico amortiguado
  • Escribir las ecuaciones de movimiento para el movimiento armónico amortiguado forzado

En el mundo real, las oscilaciones rara vez siguen el verdadero SHM. La fricción de algún tipo suele actuar para amortiguar el movimiento, de modo que desaparece, o necesita más fuerza para continuar. En esta sección, examinaremos algunos ejemplos de movimiento armónico amortiguado y veremos cómo modificar las ecuaciones de movimiento para describir este caso más general.

Una cuerda de guitarra deja de oscilar unos segundos después de ser pulsada. Para seguir balanceándose en un columpio de un parque infantil, hay que seguir empujando (Figura \(\PageIndex{1}\)). Aunque a menudo podemos hacer que la fricción y otras fuerzas no conservativas sean pequeñas o despreciables, el movimiento completamente no amortiguado es raro. De hecho, es posible que incluso queramos amortiguar las oscilaciones, como en el caso de los amortiguadores de los coches.

Una foto de una persona en un columpio
Figura (\PageIndex{1}\): Para contrarrestar las fuerzas de amortiguación, hay que seguir bombeando un columpio. (crédito: Bob Mical)

La figura \(\PageIndex{2})muestra una masa m unida a un muelle con una fuerza constante k. La masa se eleva hasta una posición A0, la amplitud inicial, y luego se suelta. La masa oscila alrededor de la posición de equilibrio en un fluido con viscosidad, pero la amplitud disminuye en cada oscilación. Para un sistema que tiene una pequeña cantidad de amortiguación, el período y la frecuencia son constantes y son casi los mismos que para SHM, pero la amplitud disminuye gradualmente como se muestra. Esto ocurre porque la fuerza de amortiguación no conservativa elimina energía del sistema, normalmente en forma de energía térmica.

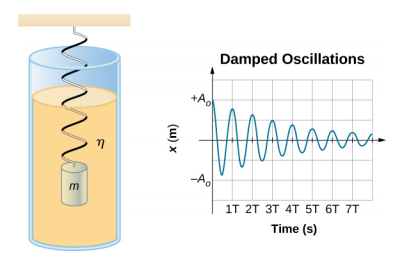
Una masa m está suspendida de un muelle vertical y sumergida en un fluido que tiene viscosidad eta. Una gráfica de la oscilación amortiguada muestra el desplazamiento x en metros en el eje vertical en función del tiempo en segundos en el eje horizontal. La escala de x va de menos A sub cero a más A sub cero. La escala de tiempo es de cero a 7 T, con tics en incrementos de T. El desplazamiento es más A sub cero en el tiempo cero y oscila entre máximos positivos y mínimos negativos, con cada ciclo completo que toma el mismo tiempo T pero la amplitud de las oscilaciones disminuye con el tiempo.
Figura (\PageIndex{2}\): Para una masa sobre un muelle que oscila en un fluido viscoso, el periodo permanece constante, pero las amplitudes de las oscilaciones disminuyen debido al amortiguamiento causado por el fluido.

Considera las fuerzas que actúan sobre la masa. Obsérvese que la única contribución del peso es cambiar la posición de equilibrio, como se ha comentado anteriormente en el capítulo. Por lo tanto, la fuerza neta es igual a la fuerza del muelle y la fuerza de amortiguación (\(F_D\)). Si la magnitud de la velocidad es pequeña, lo que significa que la masa oscila lentamente, la fuerza de amortiguación es proporcional a la velocidad y actúa en contra de la dirección del movimiento (\(F_D = -b\)). Por lo tanto, la fuerza neta sobre la masa es

Escribiendo esto como una ecuación diferencial en x, obtenemos

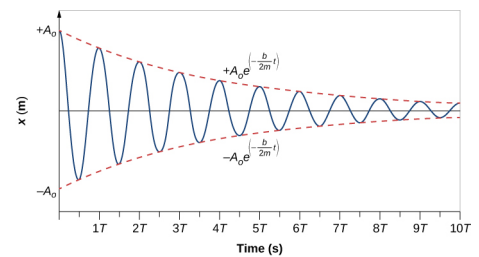
Para determinar la solución de esta ecuación, considere el gráfico de la posición frente al tiempo que se muestra en la Figura \(\PageIndex{3}\). La curva se asemeja a una curva coseno que oscila en la envolvente de una función exponencial \(A_0e^{-\alpha t}\) donde \(\alpha = \frac{b}{2m}\). La solución es

Se deja como ejercicio demostrar que ésta es, efectivamente, la solución. Para demostrar que es la solución correcta, se toman las derivadas primera y segunda con respecto al tiempo y se sustituyen en la ecuación 15.23. Se encuentra que la ecuación 15.24 es la solución si

Recuerde que la frecuencia angular de una masa que sufre SHM es igual a la raíz cuadrada de la constante de fuerza dividida por la masa. Esto se conoce a menudo como la frecuencia angular natural, que se representa como

La frecuencia angular para el movimiento armónico amortiguado se convierte en

La figura muestra un gráfico del desplazamiento, x en metros, a lo largo del eje vertical, frente al tiempo en segundos a lo largo del eje horizontal. El desplazamiento va de menos A sub cero a más A sub cero y el tiempo va de 0 a 10 T. El desplazamiento, mostrado por una curva azul, oscila entre máximos positivos y mínimos negativos, formando una onda cuya amplitud va disminuyendo gradualmente a medida que nos alejamos de t=0. El tiempo, T, entre crestas adyacentes permanece igual en todo momento. La envolvente, la curva suave que conecta las crestas y otra curva suave que conecta los valles de las oscilaciones, se muestra como un par de líneas rojas discontinuas. La curva superior que conecta las crestas está etiquetada como más A sub cero veces e a la cantidad menos b t sobre 2 m. La curva inferior que conecta los valles está etiquetada como menos A sub cero veces e a la cantidad menos b t sobre 2 m.
Figura (\PageIndex{3}\}: Posición en función del tiempo para la masa que oscila sobre un muelle en un fluido viscoso. Obsérvese que la curva parece ser una función coseno dentro de una envolvente exponencial.

Recordemos que cuando comenzamos esta descripción del movimiento armónico amortiguado, afirmamos que el amortiguamiento debe ser pequeño. Se nos ocurren dos preguntas. ¿Por qué el amortiguamiento debe ser pequeño? ¿Y qué tan pequeño es? Si aumenta gradualmente la cantidad de amortiguación en un sistema, el período y la frecuencia comienzan a verse afectados, porque la amortiguación se opone y, por lo tanto, frena el movimiento de ida y vuelta. (La fuerza neta es menor en ambas direcciones.) Si la amortiguación es muy grande, el sistema ni siquiera oscila, sino que se mueve lentamente hacia el equilibrio. La frecuencia angular es igual a

A medida que b aumenta, \ (\frac{k}{m} – \left(\dfrac{b}{2m}\right)^{2}) se hace más pequeño y finalmente llega a cero cuando b = \(\sqrt{4mk}\). Si b se hace más grande, \(\frac{k}{m} – \left(\dfrac{b}{2m}{right)^{2}) se convierte en un número negativo y \(\qrt{frac{k}{m} – \left(\dfrac{b}{2m}{right)^{2}) es un número complejo.

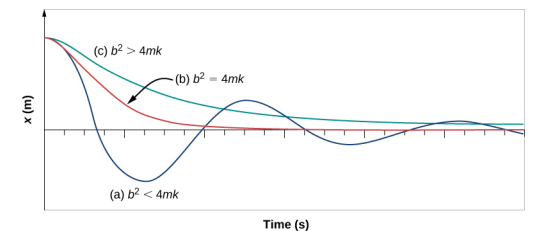
La posición, x en metros en el eje vertical, frente al tiempo en segundos en el eje horizontal, con diferentes grados de amortiguación. No se da ninguna escala para ninguno de los dos ejes. Las tres curvas comienzan en la misma posición positiva en el tiempo cero. La curva azul a, etiquetada con b al cuadrado es inferior a 4 m k, sufre algo más de dos oscilaciones y cuarto de amplitud decreciente y periodo constante. La curva roja b, etiquetada con b al cuadrado es igual a 4 m k, disminuye en t=0 menos rápidamente que la curva azul, pero no oscila. La curva roja se aproxima a x=0 asintóticamente, y es casi cero dentro de una oscilación de la curva azul. La curva verde c, etiquetada con b al cuadrado es mayor que 4 m k, disminuye en t=0 menos rápidamente que la curva roja, y no oscila. La curva verde se aproxima asintóticamente a x=0, pero sigue estando notablemente por encima de cero al final del gráfico, después de más de dos oscilaciones de la curva azul.
Figura \N(\PageIndex{4}\N): La posición frente al tiempo para tres sistemas formados por una masa y un muelle en un fluido viscoso. (a) Si el amortiguamiento es pequeño (b < \(\sqrt{4mk}\), la masa oscila, perdiendo lentamente la amplitud a medida que la energía es disipada por la(s) fuerza(s) no conservativa(s). El caso límite es (b), donde el amortiguamiento es (b = \(\sqrt{4mk}\)). (c) Si el amortiguamiento es muy grande (b > \(\sqrt{4mk}\)), la masa no oscila al desplazarse, sino que intenta volver a la posición de equilibrio.

La figura \(\PageIndex{4}) muestra el desplazamiento de un oscilador armónico para diferentes cantidades de amortiguación.

  1. Cuando la constante de amortiguación es pequeña, b <

    (\sqrt{4mk}), el sistema oscila mientras la amplitud del movimiento decae exponencialmente. Este sistema se dice que es subamortiguado, como en la curva (a). Muchos sistemas están subamortiguados, y oscilan mientras la amplitud disminuye exponencialmente, como la masa que oscila sobre un muelle. El amortiguamiento puede ser bastante pequeño, pero finalmente la masa llega al reposo.

  2. Si la constante de amortiguamiento es \ (b = \sqrt{4mk}\), se dice que el sistema está críticamente amortiguado, como en la curva (\(b\)). Un ejemplo de un sistema críticamente amortiguado son los amortiguadores de un coche. Es ventajoso que las oscilaciones decaigan lo más rápidamente posible. En este caso, el sistema no oscila, sino que se aproxima asintóticamente a la condición de equilibrio lo más rápidamente posible.
  3. La curva (c) de la figura \(\PageIndex{4}\) representa un sistema sobreamortiguado donde \(b > \sqrt{4mk}\). Un sistema sobreamortiguado se acercará al equilibrio durante un período de tiempo más largo.

    4. A menudo se desea un amortiguamiento crítico, porque un sistema de este tipo vuelve al equilibrio rápidamente y se mantiene en él también. Además, una fuerza constante aplicada a un sistema críticamente amortiguado mueve el sistema a una nueva posición de equilibrio en el menor tiempo posible sin sobrepasar u oscilar alrededor de la nueva posición.

    Ejercicio \(\PageIndex{1})

    ¿Por qué son tan raros los osciladores armónicos completamente no amortiguados?

    Contribuidores y atribuciones

    • Samuel J. Ling (Truman State University), Jeff Sanny (Loyola Marymount University), y Bill Moebs con muchos autores contribuyentes. Esta obra está licenciada por OpenStax University Physics bajo una Licencia de Atribución de Creative Commons (por 4.0).

By: adminPosted on

Deja una respuesta

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *