Definiciones estadísticas >
Análisis factorial
Contenido:
- ¿Qué es el análisis factorial?
- Cargas factoriales
- Análisis factorial múltiple
- Análisis factorial confirmatorio
- Análisis factorial exploratorio
- Qué es el Análisis Procrustes Generalizado (APG)
- ¿Qué son las variables latentes?
- ¿Qué son las Variables Manifiestas?
¿Qué es el Análisis Factorial?
El análisis factorial es una forma de tomar una masa de datos y reducirla a un conjunto de datos más pequeño que sea más manejable y comprensible. Es una forma de encontrar patrones ocultos, mostrar cómo esos patrones se superponen y mostrar qué características se ven en múltiples patrones. También se utiliza para crear un conjunto de variables para elementos similares en el conjunto (estos conjuntos de variables se denominan dimensiones). Puede ser una herramienta muy útil para conjuntos de datos complejos que incluyan estudios psicológicos, estatus socioeconómico y otros conceptos implicados. Un «factor» es un conjunto de variables observadas que tienen patrones de respuesta similares; están asociadas a una variable oculta (llamada variable de confusión) que no se mide directamente. Los factores se enumeran según las cargas factoriales, o la cantidad de variación en los datos que pueden explicar.
Los dos tipos: exploratorio y confirmatorio.
- El análisis factorial exploratorio es si no tiene ninguna idea sobre la estructura de sus datos o cuántas dimensiones hay en un conjunto de variables.
- El análisis factorial confirmatorio se utiliza para la verificación siempre que tenga una idea específica sobre qué estructura tienen sus datos o cuántas dimensiones hay en un conjunto de variables.
Cargas factoriales
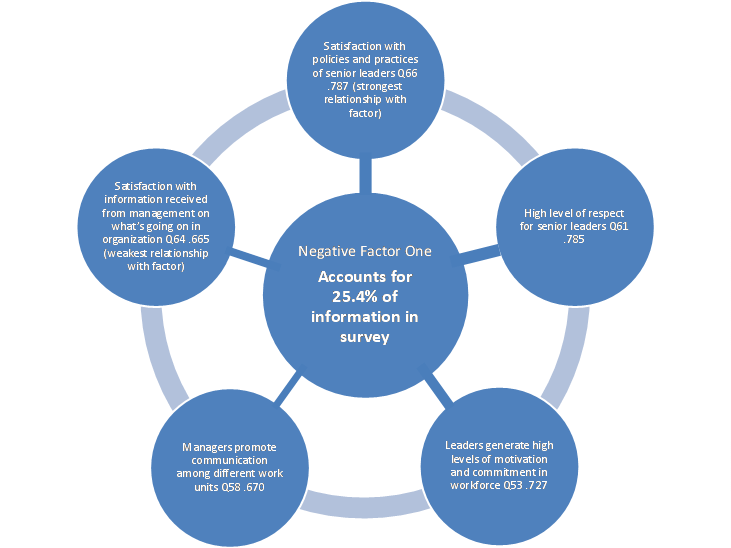
Image:USGS.gov
No todos los factores son iguales; algunos factores tienen más peso que otros. En un ejemplo sencillo, imagine que su banco realiza una encuesta telefónica de satisfacción de clientes y los resultados muestran las siguientes cargas factoriales:
| Variable | Factor 1 | Factor 2 | Factor 3 | Pregunta 1 | 0.885 | 0,121 | -0,033 |
|---|---|---|---|
| Pregunta 2 | 0,829 | 0,078 | 0,157 |
| Pregunta 3 | 0,777 | 0,190 | 0.540 |
Los factores que más afectan a la pregunta (y que, por tanto, tienen las mayores cargas factoriales) están en negrita. Las cargas factoriales son similares a los coeficientes de correlación en el sentido de que pueden variar de -1 a 1. Cuanto más cerca estén los factores de -1 o 1, más afectan a la variable. Una carga factorial de cero indicaría que no hay efecto.
Volver al principio
Análisis Factorial Múltiple
Este subconjunto del Análisis Factorial se utiliza cuando sus variables están estructuradas en grupos de variables. Por ejemplo, puede tener un cuestionario de salud para estudiantes con varios ítems como patrones de sueño, adicciones, salud psicológica o problemas de aprendizaje.
Los dos pasos que se realizan en el Análisis Factorial Múltiple son:
- El Análisis de Componentes Principales se realiza en cada conjunto de datos. Esto da un valor propio, que se utiliza para normalizar los conjuntos de datos.
- Los nuevos conjuntos de datos se fusionan en una matriz única y se realiza un segundo ACP global.
Realización del Análisis Factorial
El Análisis Factorial es un procedimiento matemático extremadamente complejo y se realiza con software.
Las instrucciones para Stata se pueden encontrar aquí.
Las instrucciones para Minitab están aquí.
Para SPSS, vea este artículo.
La prueba de Kaiser-Meyer-Olkin comprueba si sus datos son adecuados para el AF.
Volver al principio
¿Qué es el Análisis Factorial Confirmatorio?
El Análisis Factorial Confirmatorio permite a un investigador averiguar si existe una relación entre un conjunto de variables observadas (también conocidas como variables manifiestas) y sus constructos subyacentes. Es similar al Análisis Factorial Exploratorio. La principal diferencia entre ambos es:
- Si quiere explorar patrones, utilice el AFE.
- Si quiere realizar pruebas de hipótesis, utilice el AFC.
- Realice una revisión de la literatura para ayudarle a elegir un modelo apropiado. Por ejemplo, podría elegir un diagrama o ecuaciones.
- Determine si es posible un valor único para la estimación de los parámetros de la población.
- Recoja sus datos.
- Realice un análisis inicial de los datos para comprobar si hay problemas como datos faltantes, colinealidad o valores atípicos.
- Estime los parámetros de la población.
- Determine si el modelo que eligió funciona. Si el modelo es inaceptable, considere la posibilidad de realizar un Análisis Factorial Explicativo.
- Interprete sus resultados.
- Procedimiento CFA de SAS.
- Instrucciones de AMOS (descargar documento de la Universidad de Carolina del Este).
- Procedimientos de AMOS, LISREL, MPLUS.
- Evaluar la fiabilidad interna de una medida.
- Examinar factores o constructos teóricos representados por conjuntos de ítems. Asumen que los factores no están correlacionados.
- Investigar la calidad de los ítems individuales.
- Constructos o constructos hipotéticos.
- Factores.
- Variables ocultas.
- Variables hipotéticas.
- Puntuaciones verdaderas.
- Variables no medidas.
- Variables no observadas.
- Algoritmos EM.
- Análisis de factores.
- Modelos de Markov ocultos.
- Análisis semántico latente.
- Análisis de componentes principales.
- Modelado de ecuaciones estructurales.
- Heterogeneidad no observada (por ejemplo fragilidad en el análisis de supervivencia, efectos aleatorios en datos longitudinales o datos agrupados)
- Datos ausentes
- Contrafactuales o «resultados potenciales»
El AFE proporciona información sobre el número óptimo de factores necesarios para representar el conjunto de datos. Con el Análisis Factorial Confirmatorio se puede especificar el número de factores necesarios. Por ejemplo, el AFC puede responder a preguntas como «¿Mi encuesta de diez preguntas mide con precisión un factor específico?». Aunque es técnicamente aplicable a cualquier disciplina, se suele utilizar en las ciencias sociales.
Implementación del análisis factorial confirmatorio
Diane Suhr, PhD, en el sitio web de SAS, sugiere los siguientes pasos:
Según IBM, EFA ha superado a CFA como medio de Análisis Factorial. «El enfoque de AFC predominante hoy en día es considerar el AFC como un caso especial del modelado de ecuaciones estructurales (SEM). Se especifican las cargas de los factores como un conjunto de declaraciones de regresión desde el factor a las variables observadas». Con el EFA, es posible especificar unos pocos factores y una rotación particular; entonces puede comparar sus resultados para ver si se ajustan a su modelo.
Realización de CFA
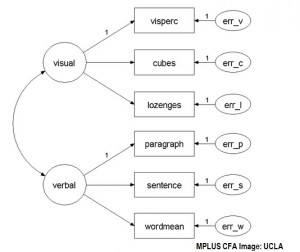
Por lo general, se requiere un software para realizar el análisis factorial confirmatorio. Se puede utilizar SAS para realizar el AFC. En el momento de escribir este artículo, SPSS se limita sólo a EFA.
Volver al principio
¿Qué es el análisis factorial exploratorio?
El análisis factorial exploratorio (AFE) se utiliza para encontrar la estructura subyacente de un gran conjunto de variables. Reduce los datos a un conjunto mucho más pequeño de variables de resumen.
EFA es casi idéntico al análisis factorial confirmatorio (CFA). Ambas técnicas pueden (quizás sorprendentemente) ser utilizadas para confirmar o explorar. Las similitudes son:
Sin embargo, existen algunas diferencias, sobre todo en lo que respecta a cómo se tratan/utilizan los factores. EFA es básicamente un enfoque basado en los datos, que permite que todos los ítems se carguen en todos los factores, mientras que con CFA se debe especificar qué factores se cargan. El AFE es una buena opción si no se tiene ninguna idea sobre los factores comunes que pueden existir. El AFE puede generar un gran número de modelos posibles para sus datos, algo que no sería posible si un investigador tuviera que especificar los factores. Si tiene una idea sobre el aspecto de los modelos y quiere probar sus hipótesis sobre la estructura de los datos, el AFC es un mejor enfoque.
¿Qué es el Análisis de Procrustes Generalizado (APG)?
El análisis de Procrustes es una forma de comparar dos conjuntos de configuraciones, o formas. Desarrollado originalmente para comparar dos soluciones del Análisis Factorial, la técnica se extendió al Análisis Procrustes Generalizado para poder comparar más de dos formas. Las formas se alinean con una forma objetivo o entre sí.
GPA utiliza transformaciones geométricas (es decir, reescalado isotrópico, reflexión, rotación o traslación) de matrices para comparar los conjuntos de datos. La siguiente imagen muestra una serie de transformaciones sobre un triángulo objetivo verde.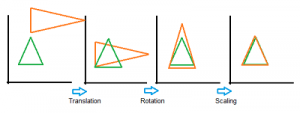
La matriz de consenso es (como su nombre indica), el resultado de los promedios de todas las matrices de entrada. Las matrices formadas durante el proceso de Análisis de Procrustes Generalizado pueden ser introducidas en el Análisis de Componentes Principales y proyectadas en un espacio bidimensional para obtener resultados fácilmente comprensibles.
Uso en Perfiles Sensoriales
El Análisis de Procrustes Generalizado una forma de encontrar una estructura subyacente en los perfiles sensoriales, que se dividen en dos categorías: perfiles convencionales y perfiles de libre elección.
Con los perfiles convencionales, se proporciona un conjunto fijo de términos descriptivos a los evaluadores. Los evaluadores suelen ser personas altamente capacitadas. Por ejemplo, se puede pedir a tres expertos su opinión sobre el cuerpo, el aroma y el sabor de cuatro marcas de vino. Las descripciones fijas podrían incluir crujiente, anguloso y mantecoso. Los resultados pueden promediarse, por lo que es posible utilizar el Análisis Factorial o el Análisis de Componentes Principales -así como el GPA- para analizar la prueba.
La elaboración de perfiles de libre elección da a los encuestados la libertad de responder a las preguntas con sus propios términos descriptivos. Como no hay términos fijos que promediar, no es posible utilizar el Análisis Factorial o el PCA. En este tipo de perfiles de libre elección se utilizan métodos de conjuntos K, como el PCA.
Las categorías son las dimensiones del Análisis de Procrustes Generalizado. Idealmente, el número de dimensiones es igual en todo el tablero (en este ejemplo, eso significaría que el experto dio una calificación en las tres áreas). Sin embargo, es posible ejecutar el Análisis Procrustes Generalizado utilizando dimensiones desiguales.
Volver al principio
¿Qué son las variables latentes?
Una variable latente o «oculta» se considera generalmente como una variable que no es directamente medible u observable. Por ejemplo, el nivel de neurosis de una persona, la conciencia o la apertura son variables latentes. Aunque no se pueden ver estas variables subyacentes (no forman parte del conjunto de datos de un experimento), pueden causar efectos en los resultados experimentales. Las variables latentes también se conocen como:
Uno de los primeros ejemplos de variable latente se publicó en 1904 cuando Spearman midió la inteligencia utilizando el análisis factorial. A veces se utiliza una definición más precisa de las variables latentes. Por ejemplo, MacCallum & Austin(2000) describe estas variables como «constructos hipotéticos que no pueden medirse directamente». Son hipotéticas porque sólo existen en la mente del investigador.
La variable latente en el modelado estadístico
Las variables latentes se utilizan a veces en técnicas de modelado estadístico como el análisis factorial, donde pueden inferirse mediante técnicas de modelado. Las variables latentes están siempre presentes en casi todos los análisis de regresión, porque todos los términos de error aditivos no son medibles (y por lo tanto son latentes).
Los métodos de modelado estadístico que se utilizan a menudo para identificar las variables latentes incluyen:
Una variable latente también puede estar presente (e incluirse en un modelo) cuando no hay objetivo de medirla realmente. Melanie Wall, de la Universidad de Columbia, ofrece los siguientes tres ejemplos de variables latentes que no pretenden ser medidas:
Volver al principio
¿Qué son las variables manifiestas?
Las variables manifiestas (también llamadas variables observables) se pueden medir u observar directamente. Son lo contrario de las variables latentes. Por ejemplo, la edad y el género son variables observables. Sin embargo, es raro que se pueda estar 100% seguro de una variable; incluso el «género», si se observa, no es 100% seguro, porque la gente puede mentir en su formulario, disfrazar su verdadero género o ser una persona transgénero. Por lo tanto, debe utilizar variables latentes siempre que sea posible.
Referencia:
MacCallum RC, Austin JT. 2000. Aplicaciones de los modelos de ecuaciones estructurales en la investigación psicológica. Annu. Rev. Psychol. 51:
201-26
Stephanie Glen. «Análisis de factores: Definición fácil» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/factor-analysis/
——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!