Antecedentes
La Criptografía de Curvas Elípticas (ECC) es una aproximación a la criptografía de clave pública, basada en la estructura algebraica de las curvas elípticas sobre campos finitos. ECC requiere una clave más pequeña en comparación con la criptografía no ECC para proporcionar una seguridad equivalente (una seguridad ECC de 256 bits tiene una seguridad equivalente a la obtenida por la criptografía RSA de 3072 bits).
Para una mejor comprensión de la Criptografía de Curva Elíptica, es muy importante entender los fundamentos de la Curva Elíptica. Una curva elíptica es una curva algebraica plana definida por una ecuación de la forma
![]()
Donde ‘a’ es el coeficiente de x y ‘b’ es la constante de la ecuación
La curva es no sinular; es decir, su gráfica no tiene cúspides ni autointersecciones (cuando la característica del campo Coeficiente es igual a 2 ó 3).
En general, una curva elíptica tiene el aspecto que se muestra a continuación. Las curvas elípticas podrían intersecarse en casi 3 puntos cuando se traza una línea recta que interseca la curva. Como podemos ver la curva elíptica es simétrica respecto al eje x, esta propiedad juega un papel clave en el algoritmo.
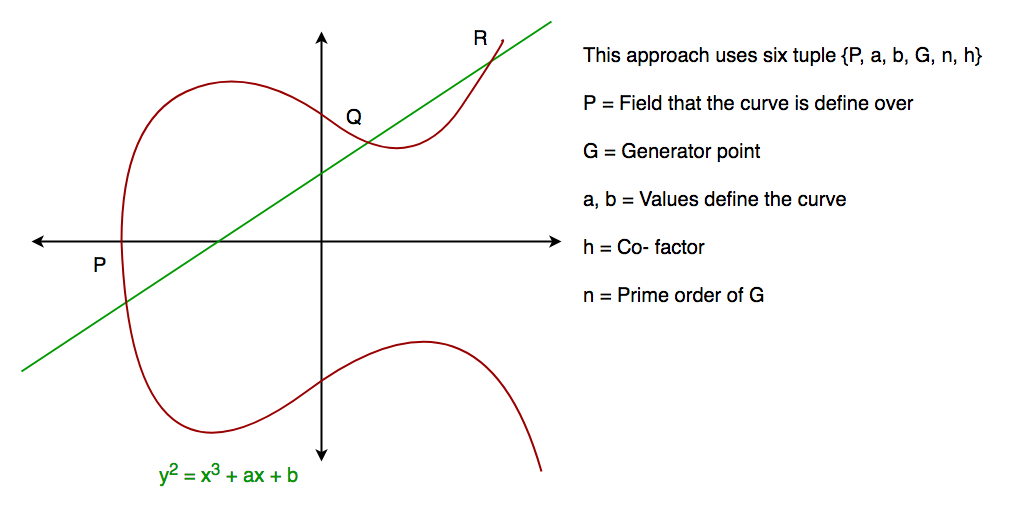
Algoritmo de Diffie-Hellman
El algoritmo de Diffie-Hellman se utiliza para establecer un secreto compartido que puede ser utilizado para comunicaciones secretas mientras se intercambian datos a través de una red pública utilizando la curva elíptica para generar puntos y obtener la clave secreta utilizando los parámetros.
- Para simplificar la implementación práctica del algoritmo, consideraremos sólo 4 variables un primo P y G (una raíz primitiva de P) y dos valores privados a y b.
- P y G son números disponibles públicamente. Los usuarios (digamos Alicia y Bob) eligen los valores privados a y b y generan una clave y la intercambian públicamente, la persona contraria recibe la clave y a partir de ella genera una clave secreta tras lo cual tienen la misma clave secreta para cifrar.
Explicación paso a paso
| Alice | Bob | |
|---|---|---|
| Claves públicas disponibles = P, G | Claves públicas disponibles = P, G | |
| Clave privada seleccionada = a | Clave privada seleccionada = b | |
| Clave generada =
|
Clave generada =
|
|
| Se produce el intercambio de claves generadas | ||
| Clave recibida = y | Clave recibida = x |
Clave secreta generada =
|
Clave secreta generada =
|
|
Algebraicamente se puede demostrar que
|
||
| Los usuarios tienen ahora una clave secreta simétrica para cifrar | ||
Ejemplo
Step 1: Alice and Bob get public numbers P = 23, G = 9Step 2: Alice selected a private key a = 4 and Bob selected a private key b = 3Step 3: Alice and Bob compute public valuesAlice: x =(9^4 mod 23) = (6561 mod 23) = 6 Bob: y = (9^3 mod 23) = (729 mod 23) = 16Step 4: Alice and Bob exchange public numbersStep 5: Alice receives public key y =16 and Bob receives public key x = 6Step 6: Alice and Bob compute symmetric keys Alice: ka = y^a mod p = 65536 mod 23 = 9 Bob: kb = x^b mod p = 216 mod 23 = 9Step 7: 9 is the shared secret.
Implementación:
#include<stdio.h>
#include<math.h>longlongintpower(longlonginta, longlongintb,
longlongintP) {
if(b == 1) returna;
else
return(((longlongint)pow(a, b)) % P); }intmain()
{ longlongintP, G, x, a, y, b, ka, kb;
P = 23;
printf("The value of P : %lld\n", P); G = 9;
printf("The value of G : %lld\n\n", G);
a = 4;
printf("The private key a for Alice : %lld\n", a);
x = power(G, a, P);
b = 3;
printf("The private key b for Bob : %lld\n\n", b);
y = power(G, b, P);
ka = power(y, a, P);
kb = power(x, b, P);
printf("Secret key for the Alice is : %lld\n", ka);
printf("Secret Key for the Bob is : %lld\n", kb); return0;
}fromrandom importrandint
if__name__ =='__main__':
P =23
G =9
print('The Value of P is :%d'%(P)) print('The Value of G is :%d'%(G))
a =4
print('The Private Key a for Alice is :%d'%(a)) x =int(pow(G,a,P))
b =3
print('The Private Key b for Bob is :%d'%(b))
y =int(pow(G,b,P))
ka =int(pow(y,a,P))
kb =int(pow(x,b,P)) print('Secret key for the Alice is : %d'%(ka)) print('Secret Key for the Bob is : %d'%(kb))
Salida
The value of P : 23The value of G : 9The private key a for Alice : 4The private key b for Bob : 3Secret key for the Alice is : 9Secret Key for the Bob is : 9
Este artículo es una contribución de Souvik Nandi. Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando contribute.GeeksforGeeks.org o enviar tu artículo por correo a [email protected]. Verás cómo tu artículo aparece en la página principal de GeeksforGeeks y ayudarás a otros Geeks.
Por favor, escribe comentarios si encuentras algo incorrecto, o quieres compartir más información sobre el tema tratado anteriormente.