قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).
Definición

La ley de Bragg proporciona la condición para que una onda plana sea difractada por una familia de planos de la red:
2 d sin θ = n λ
donde d es la separación interplanar, θ el ángulo entre el vector de onda de la onda plana incidente, ko, y los planos de la red, λ su longitud de onda y n es un número entero, el orden de la reflexión. Es equivalente a la condición de difracción en el espacio recíproco y a las ecuaciones de Laue.
Derivación directa de la ley de Bragg
- Reflexión desde el primer plano
Las ondas dispersas estarán en fase sea cual sea la distribución de los dispersores puntuales en el primer plano si el ángulo del vector de onda reflejado, kh, es también igual a θ. Esta es la ley de reflexión de Snell-Descartes.
- Reflexión desde el segundo plano
Dado que la fase de las ondas reflejadas es independiente de la posición del dispersor puntual en el plano, la diferencia de fase entre las ondas reflejadas por dos planos sucesivos de la red se obtiene eligiendo arbitrariamente un punto de dispersión, A, en el primer plano y un punto de dispersión, B, en el segundo plano tales que AB es normal a los planos. Si C y D son las proyecciones de A sobre los vectores de onda incidente y reflejada que pasan por B, se deduce de la figura 1 que la diferencia de trayectoria entre las ondas reflejadas en A y B, respectivamente, es:
CB + BD = 2d sin θ
y que las dos ondas estarán en fase si esta diferencia de trayectoria es igual a nλ donde n es un número entero.
- Reflexión desde el tercer, etc. plano
Si la relación de Bragg se satisface para los dos primeros planos, las ondas reflejadas con el vector de onda kh estarán en fase para todos los planos de la familia.
Orden de la reflexión
La ley de Bragg también puede escribirse:
2 (d/n) sin θ = λ.
Se puede decir entonces que una reflexión de Bragg de orden n en una familia de planos de celosía de orden n es equivalente a una reflexión de orden 1 en una familia de planos ficticios, o imaginarios, de separación de celosía
d_{hkl} = d/n.
Esta familia ficticia está asociada al vector reticular recíproco OH donde OH = n/d = 1/d_{hkl}. Los índices de la reflexión son hkl. Por ejemplo, las líneas horizontales discontinuas de la figura 1 corresponden a los planos ficticios asociados al segundo orden, n = 2.
Condiciones de reflexión
Si hay un plano de deslizamiento o un eje de tornillo normal a los planos de la red, la separación de los planos de reflexión reales es d/2 para un plano de deslizamiento y (d p/q) para un eje de tornillo qp. La ley de Bragg debe entonces escribirse:
2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ
para un plano de deslizamiento y
2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ
para un eje de tornillo qp.
Las reflexiones de orden impar para un plano de deslizamiento y de orden diferente de (q/p)n para un eje de tornillo están entonces ausentes. Se habla de ausencias sistemáticas relacionadas con la presencia de componentes de deslizamiento o de tornillo.
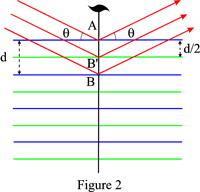
A modo de ejemplo, la figura 2 muestra el caso de un eje de tornillo 21: los planos reflectantes son los planos azules y los planos verdes deducidos de estos últimos por la acción del eje de tornillo. Las reflexiones de orden impar estarán sistemáticamente ausentes.
Influencia de la deformación
Una deformación que deje sin distorsión una familia de planos de la red (hkl) y su espaciado de red d sin cambios no afectará al ángulo de Bragg de las reflexiones kkl, por ej.Por ejemplo, los planos de la red paralelos a las dislocaciones de un tornillo.
Historia
Bragg (1890-1971) presentó su derivación de la condición de reflexión en una reunión de la Sociedad Filosófica de Cambridge el 11 de noviembre de 1912. Su artículo se publicó en 1913. Para más detalles, véase P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Sección 5, p. 64 y A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Sección 6.11, p. 120.
Véase también
- Ecuaciones de Laue
.