Tasas de error por familias > Holm-Método Bonferroni
Es posible que quiera leer este artículo primero: Tasas de error por familias.
¿Qué es el Método Holm-Bonferroni?
El Método Holm-Bonferroni (también llamado Procedimiento Secuencial de Bonferroni de Holm) es una forma de tratar las tasas de error por familias (FWER) para las pruebas de hipótesis múltiples. Es una modificación de la corrección de Bonferroni. La corrección de Bonferroni reduce la posibilidad de obtener un resultado estadísticamente significativo (es decir, un error de tipo I) al realizar pruebas múltiples. Aunque el Bonferroni es sencillo de calcular, adolece de falta de potencia estadística. El método Holm-Bonferroni también es bastante sencillo de calcular, pero es más potente que el Bonferroni de un solo paso.
Fórmula
La fórmula para calcular el Holm-Bonferroni es: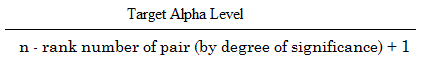
Donde:
- Nivel alfa objetivo = nivel alfa global (normalmente .05),
- n = número de pruebas.
- H1 = 0.01.
- H2 = 0,04
- H3 = 0,03
- H4 = 0,005
- H4 = 0.005
- H1 = 0,01
- H3 = 0,03
- H2 = 0,04
El siguiente ejemplo muestra cómo funciona la fórmula.
Ejemplo
Pregunta: Utilice el método Holm-Bonferroni para probar las siguientes cuatro hipótesis y sus valores p asociados a un nivel alfa de .05:
Nota: ya conocemos los valores p asociados a cada hipótesis. Si no conoce los valores p, realice una prueba para cada hipótesis antes de intentar ajustar el FWER mediante el método Holm-Bonferroni.
Paso 1: Ordene los valores p de menor a mayor:
Paso 2: Trabajar la fórmula de Holm-Bonferroni para el primer rango:
HB = Objetivo α / (n – rango + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.
Paso 3: Compare el valor p del primer rango (el más pequeño) del Paso 1 con el nivel alfa calculado en el Paso 2:
El valor p más pequeño, en el Paso 1 (H4 = 0.005) <Nivel alfa en el Paso 2 (.0125).
Si el valor p es menor, rechace la hipótesis nula para esta prueba individual.
El valor p de .005 es menor que .0125, por lo que se rechaza la hipótesis nula para H4.
Paso 4: Repita la fórmula HB para el segundo rango .
HB = Objetivo α / (n – rango + 1)
HB = 0,05 / 4 – 2 + 1 = 0,05 / 3 = 0,0167
Paso 5: Compare el resultado de la fórmula HB del paso 4 con el valor p del segundo rango:
Segundo valor p clasificado, en el Paso 1 (H1 = 0,01) < Nivel alfa en el Paso 2 (,0167).
El valor p de 0,01 es menor que 0,0167, por lo que también se rechaza la hipótesis nula de H1.
Paso 6: Repita la fórmula HB para el tercer rango.
HB = Objetivo α / (n – rango + 1)
HB = 0,05 / 4 – 3 + 1 = 0,05 / 2 = 0,025
Paso 7: Compare el resultado de la fórmula HB del Paso 6 con el valor p del tercer rango:
Tercer valor p clasificado, en el Paso 1 (H3 = 0,03) > Nivel alfa en el Paso 6 (.025).
El valor p de .03 es mayor que .025, por lo que la hipótesis nula para H3 no se rechaza.
La prueba se detiene cuando se llega a la primera hipótesis no rechazada. Todas las hipótesis posteriores son no significativas (es decir, no se rechazan).
Referencia:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70
Stephanie Glen. «Método Holm-Bonferroni: Paso a paso» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/holm-bonferroni-method/
——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!