Introducción

El pandeo de columnas es un tema curioso y único. Es quizá el único campo de la mecánica estructural en el que el fallo no está relacionado con la resistencia del material. Pero en el caso de los pilares largos, el colapso no tiene nada que ver con la resistencia del material. En cambio, se rige por la rigidez de la columna, tanto material como geométrica.
En esta página se derivarán las ecuaciones estándar del pandeo de la columna utilizando dos enfoques.En primer lugar, se cubrirá el desarrollo habitual de las ecuaciones, es decir, la teoría de pandeo de Euler. Esta es la derivación que se encuentra en los libros de texto y se presenta en los cursos de ingeniería. Pero nunca me ha gustado. No porque sea incorrecta (es correcta), sino porque no creo que presente satisfactoriamente los mecanismos físicos que rigen el proceso de pandeo. Por eso también se presentará una segunda derivación de las ecuaciones de pandeo.
Curiosamente, los objetos se denominan columnas cuando se cargan axialmente en compresión, como es el caso, pero se denominan vigas cuando se cargan transversalmente.No obstante, la teoría de la flexión de las vigas es fundamental para los análisis de pandeo de las columnas, por lo que se recomienda al lector que revise esta página de flexión de las vigas.
Teoría de pandeo de Euler
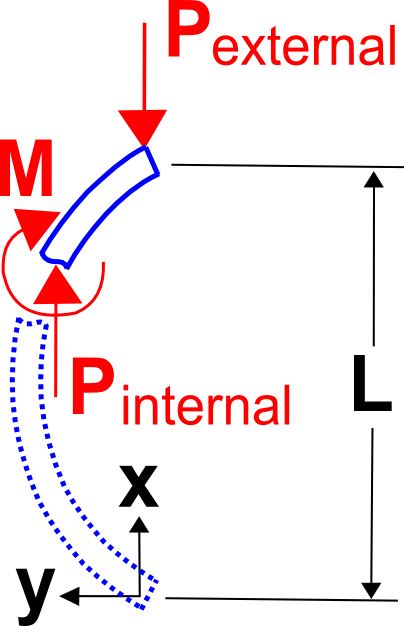
La teoría de pandeo de Euler es la teoría clásica presentada en los libros de texto y en las aulas. Comienza simplemente observando que el momento flector interno en una columna cargada y deformada es \(-P \, y\) donde \(P\) es la carga de compresión y \(y\) es la deflexión de la columna. Así que inserte \(-P \, y\) en lugar de \(M\) en la ecuación de flexión de la viga, \( E \, I \, y» = M \).
Esto produce la siguiente ecuación diferencial
que tiene la solución
donde \(A\) y \(B\) son constantes determinadas a partir de las condiciones de contorno.
Las condiciones de contorno son \(y = 0\) en \(x = 0\) y \(x = L\).
La primera condición de contorno, \(y = 0\) en \(x = 0\), lleva a la conclusión de que \(B = 0\). Y esto nos deja
Hasta aquí, todo bien. Pero es en este punto donde la derivación clásica tiende a dejar de lado la intuición física y se vuelve abiertamente matemática…
Las cosas se ponen muy interesantes con la 2ª condición de contorno porque, como veremos, no conduce a la determinación de la constante desconocida, \N(A\). Para ver esto, inserte la segunda condición de contorno de la siguiente manera.
Hay básicamente dos posibilidades aquí. En el primer caso, \(A = 0\), pero esto es aburrido porque conduce al resultado de que todos los desplazamientos son cero. Esta es sólo la solución sin pandeo. Antes de que la columna se pandee, sus desplazamientos laterales son simplemente cero.
El segundo caso es el interesante, y el que está directamente relacionado con el pandeo de la columna. El segundo método para satisfacer la condición de contorno es observar que \(\sin(\pi) = 0\). Por lo tanto, la forma de satisfacer la condición de contorno es requerir que el argumento de la ecuación, (\left( \sqrt{{P \over E \}}, I} \}; L \right)\) debe ser igual a \\pi).Haciendo esto se obtiene
y resolviendo para \(P\) se obtiene
Este es el resultado clásico de la teoría de pandeo de Euler. Da el valor crítico de la carga \ (P\), llamado \ (P_{cr}\), por encima del cual, la columna se doblará.
Este resultado es perfectamente legítimo. Sin embargo, como debería ser evidente a estas alturas, es muy matemático por naturaleza, y proporciona poca información física como resultado. La siguiente derivación presentará un método alternativo para llegar a la misma ecuación que creo que proporciona una conexión física mucho más directa con el proceso de pandeo que la derivación anterior.

Flexión vs. Cesión
Como se ha dicho al principio, el análisis clásico de la flexión es independiente del límite elástico de un material. Esto es evidente en la derivación anterior, ya que en ningún momento se habló de la tensión o la deformación ni se comparó con la resistencia de un material.
Pero, de hecho, las consideraciones sobre el límite elástico nunca deben ser totalmente ignoradas. Una vez que se obtiene una estimación de (P_{cr}) a partir de la ecuación anterior, siempre se debe dividir por el área de la sección transversal de la columna, (A), para obtener una tensión y comparar este valor con el límite elástico del material para determinar si se producirá la fluencia antes del pandeo. Esto es fundamental para los pilares cortos, ya que tienen valores inherentemente altos de \N(P_{cr}\N porque \N(L^2\N) está en el denominador de la ecuación de pandeo.

Las restricciones finales en el pandeo
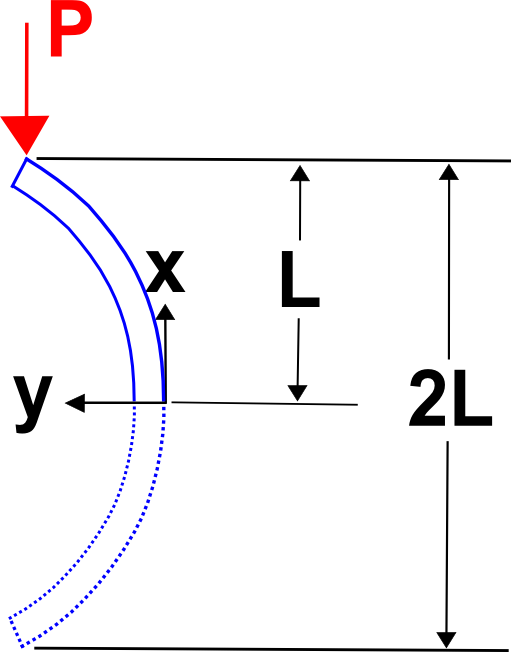
Aunque no es el objetivo de esta página, es importante reconocer que las restricciones de los extremos son críticas para los análisis de pandeo porque alteran el valor de \ (P_{cr}\). Por ejemplo, considere que la carga crítica de pandeo de la columna que se muestra aquí está dada por
Nótese que este valor es 1/4 del dado en la ecuación anterior para \(P_{cr}\).Pero es fácil ver por qué. El esquema muestra que la condición de pandeo aquí es exactamente equivalente al pandeo de una columna de dos veces la longitud y teniendo las mismas condiciones de contorno que en la derivación anterior. Y esto nos lleva a
Derivación del pandeo con base física
Esta sección presentará un método alternativo para determinar las cargas críticas de pandeo que creo que es más intuitivo físicamente que la teoría clásica de pandeo de Euler. Su característica principal es la comparación del momento flector interno derivado de la distribución de tensiones internas con el momento flector externo resultante de la carga aplicada al pilar. (La frase anterior es crítica.)
Este enfoque retoma aproximadamente el punto en el que se señaló anteriormente que el enfoque clásico de Euler se vuelve abiertamente matemático. El primer paso es suponer una forma deformada. Sabemos que \(y = 0\) en ambos extremos de la columna, y que la forma sigue una función \(\sin()\) basada en la ecuación diferencial abovedada. Por lo tanto, la opción más lógica es
donde \(\delta_{max}\) es el desplazamiento lateral en el punto medio de la columna. Su valor es desconocido, pero se sabe que es mayor en el punto medio que en cualquier otro punto de la columna, de ahí el subíndice \(max). La elección de \(\pi x / L\) como argumento de la función \(\sin()\) asegura que los desplazamientos son nulos en \(x = 0\) y \(x = L\). (Hablaremos de otras formas asumidas en breve.)

Si te preguntas por el término \(\sqrt{P/EI}\ en la función\(\sin()\) de la anterior solución de Euler, no lo hagas. Surgió de la solución de la ecuación diferencial, pero aquí pretendemos no saber nada de los detalles de esa solución (¡alerta de excepción!).Sólo necesitamos una función que pueda parecerse a una columna arqueada con desplazamientos nulos en sus extremos. El uso de \(\sin ( {\pi x \over L} )\a) lo consigue.
La «alerta de excepción» está presente arriba porque estamos aprovechando una pieza de conocimiento sobre el análisis anterior. Es que las funciones trigonométricas son las soluciones de la ecuación diferencial.Por lo tanto, los senos y cosenos deben ser utilizados siempre que sea posible para describir las formas deformadas porque conducirán a las estimaciones más precisas de \ {P_{cr}\}.
Recordemos de la teoría de flexión de vigas que el momento flector, \(M\), está relacionado con la deflexión del pilar por
Aunque no es crítico, es útil recordar que esta relación proviene del cálculo del momento en la sección transversal debido a la distribución de esfuerzos. La relación muestra que necesitamos la segunda derivada de la función de desplazamiento supuesta.
Este es el momento flector interno en la columna debido a la distribución de tensiones en su interior, que a su vez se debe al hecho de que la columna está doblada.
Aquí viene una idea importante… Este momento de flexión puede considerarse como la resistencia interna de la columna a la flexión, o la fuerza con la que trata de enderezarse.
El siguiente paso es equiparar este momento de flexión de resistencia interna con el resultante de la carga externa. Esa cantidad es simplemente (M = -P, y(x)-). Al igualar los dos resultados se obtiene
No es difícil ver en este punto que este enfoque conduce a la misma expresión para \(P_{cr}\) que la teoría clásica de pandeo de Euler.Pero en el camino, ha proporcionado mucha más información sobre el proceso físico de pandeo que la teoría anterior. A saber…
- Hemos llegado a esta relación equiparando el momento flector interno (debido a las tensiones internas derivadas de la flexión de la columna) con el momento flector externo resultante de la carga externa, \(P\).Debe quedar claro que el pandeo se produce cuando \(P\) es lo suficientemente grande para satisfacer la ecuación. Cualquier valor inferior, y \ (P \, y(x)\) será menor que el «momento flector resistente».
- El hecho de que \ (y(x)\) aparezca en ambos lados de la ecuación, y por tanto se anule, significa que cuando se produce el pandeo, lo hace simultáneamente en toda la longitud de la columna. (Un resultado fascinante que no es evidente en la teoría de Euler.)
De todos modos, anulando \(y(x)\) de ambos lados de la ecuación se obtiene
\
de nuevo, pero con una visión mucho más física esta vez.

Ejemplo de extremo fijo
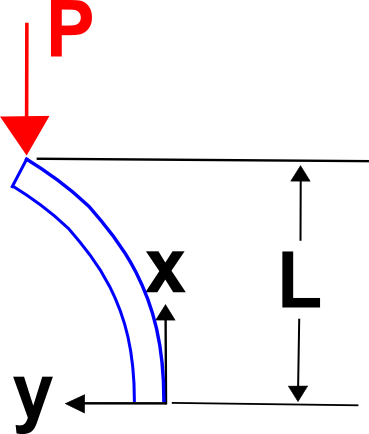
Esta vez, supongamos una forma deformada de
Calcular el momento flector debido a esto.
El momento flector debido a la carga externa es \(M = P ( \delta_{max} – y(x) )\N-). Igualando estos dos y simplificando se obtiene el resultado conocido.
\

Ejemplo de extremo fijo con diferente forma asumida
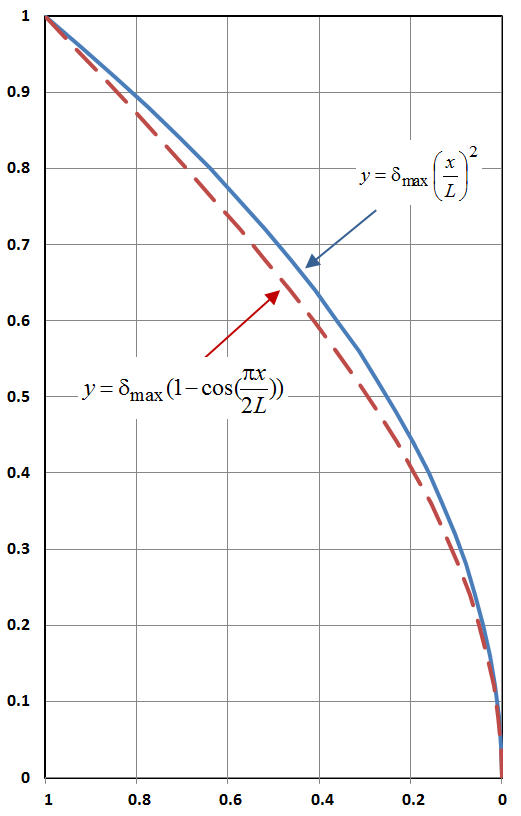
Este ejemplo demostrará que se pueden asumir funciones alternativas para la forma deformada de la columna, y que la fórmula resultante para \ {P_{cr}} no será significativamente diferente de la soluciónexacta.
Esta vez, suponga una forma deformada de
Calcule el momento flector debido a ésta.
El momento flector debido a la carga externa sigue siendo \(M = P ( \delta_{max} – y(x) )\N-). Al igualar estos dos resultados se obtiene
De la ecuación se desprende que el valor mínimo de \(P\) se producirá en \(x = 0\)ya que es en este punto donde \(y(x)\Nes un mínimo (cero, de hecho) y por lo tanto((\delta_{max} – y(x))\Nes un máximo. Fijando \(y(x)\Nen cero y cancelando(\delta_{max}) de ambos lados se obtiene
Es interesante notar que esta solución basada en la forma cuadrática, condujo a una carga crítica de pandeo menor y a una concentración de la falla por pandeo en la base de la columna, \(x = 0\).Por el contrario, la solución exacta consistente en la función trigonométrica, producía una tendencia al pandeo igual a lo largo de toda la longitud del pilar, y un correspondiente mayor \ {P_{cr}}.
Un factor clave aquí es que la forma deformada cuadrática asumida no es una solución exacta de la ecuación diferencial gobernante (aunque está cerca). Las funciones Trig sí lo son.