Théorie des graphes >

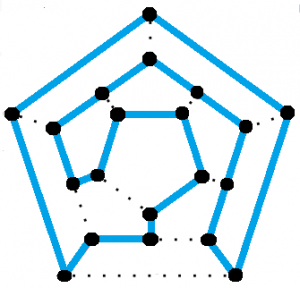
Un dodécaèdre ( une figure solide régulière à douze faces pentagonales égales) possède un cycle hamiltonien.

Un cycle hamiltonien est une boucle fermée sur un graphe où chaque nœud (sommet) est visité exactement une fois.

Une boucle est juste une arête qui joint un nœud à lui-même ; ainsi un cycle hamiltonien est un chemin voyageant d’un point à lui-même, visitant chaque nœud en route.

Si un graphe comportant plus d’un nœud (c’est-à-dire un graphe non squelettique) possède ce type de cycle, nous l’appelons un graphe hamiltonien.

Il n’existe pas d’équation ou d’astuce générale pour savoir si un graphe possède un cycle hamiltonien ; la seule façon de le déterminer est de faire une recherche complète et exhaustive, en passant par toutes les options.

Histoire du cycle hamiltonien

Le cycle a été nommé d’après Sir William Rowan Hamilton qui, en 1857, a inventé un jeu de réflexion qui consistait à chasser un cycle hamiltonien. Le jeu, appelé jeu icosien, était distribué sous la forme d’un graphe en dodécaèdre avec un trou à chaque sommet. Pour résoudre l’énigme ou gagner le jeu, il fallait utiliser des chevilles et une ficelle pour trouver le cycle hamiltonien – une boucle fermée qui visitait chaque trou exactement une fois. La solution est présentée dans l’image ci-dessus.

Exemples de graphes hamiltoniens

Tout graphe complet ayant plus de deux sommets est un graphe hamiltonien. Cela découle de la définition d’un graphe complet : un graphe simple non dirigé tel que chaque paire de nœuds est reliée par une arête unique.

Le graphe de chaque solide platonique est un graphe hamiltonien. Ainsi, le graphe d’un cube, d’un tétraèdre, d’un octaèdre ou d’un icosaèdre sont tous des graphes hamiltoniens avec des cycles hamiltoniens.

Un graphe à n sommets (où n > 3) est hamiltonien si la somme des degrés de chaque paire de sommets non adjacents est égale ou supérieure à n. C’est ce qu’on appelle le théorème d’Ore.

Applications des cycles hamiltoniens et des graphes

La recherche de ces cycles n’est pas seulement un jeu amusant pour l’après-midi de congé. Elle a des applications réelles dans des domaines aussi divers que l’infographie, la conception de circuits électroniques, la cartographie des génomes et la recherche opérationnelle.

Par exemple, lors de la cartographie des génomes, les scientifiques doivent combiner de nombreux petits fragments de code génétique (« lectures », on les appelle), en une seule séquence génomique (une « superstring »). Cela peut être fait en trouvant un chemin ou un cycle hamiltonien, où chacune des lectures est considérée comme des nœuds dans un graphe et chaque chevauchement (endroit où la fin d’une lecture correspond au début d’une autre) est considéré comme une arête.

Dans une application beaucoup moins complexe d’exactement les mêmes mathématiques, les districts scolaires utilisent les hamiltoniens pour planifier le meilleur itinéraire pour ramasser les élèves de tout le district. Ici, les élèves peuvent être considérés comme des nœuds, les chemins entre eux comme des arêtes, et le bus souhaite emprunter un itinéraire qui passera exactement une fois devant la maison de chaque élève.

Jeu icosien
Sur les cycles hamiltoniens et les chemins hamiltoniens
Assemblage de génomes
Graph Algorithmes in Bioinformatics

——————————————————————————

Vous avez besoin d’aide pour un devoir ou une question de test ? Avec Chegg Study, vous pouvez obtenir des solutions étape par étape à vos questions de la part d’un expert en la matière. Vos 30 premières minutes avec un tuteur Chegg sont gratuites !