Teoria del grafico >

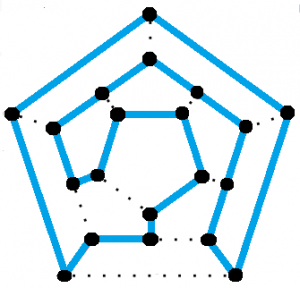
Un dodecaedro (una figura solida regolare con dodici facce pentagonali uguali) ha un ciclo hamiltoniano.

Un ciclo hamiltoniano è un ciclo chiuso su un grafo in cui ogni nodo (vertice) è visitato esattamente una volta.

Un ciclo è solo un bordo che unisce un nodo a se stesso; così un ciclo hamiltoniano è un percorso che viaggia da un punto a se stesso, visitando ogni nodo lungo il percorso.

Se un grafo con più di un nodo (cioè un grafo non singoletto) ha questo tipo di ciclo, lo chiamiamo un grafo hamiltoniano.

Non c’è nessuna equazione o trucco generale per scoprire se un grafo ha un ciclo hamiltoniano; l’unico modo per determinarlo è fare una ricerca completa ed esaustiva, passando attraverso tutte le opzioni.

Storia del ciclo hamiltoniano

Il ciclo prende il nome da Sir William Rowan Hamilton che, nel 1857, inventò un gioco-puzzle che consisteva nel cercare un ciclo hamiltoniano. Il gioco, chiamato Icosian game, era distribuito come un grafico a dodecaedro con un buco in ogni vertice. Per risolvere l’enigma o vincere il gioco si dovevano usare pioli e spago per trovare il ciclo hamiltoniano – un ciclo chiuso che visitava ogni buco esattamente una volta. La soluzione è mostrata nell’immagine qui sopra.

Esempi di grafi hamiltoniani

Ogni grafico completo con più di due vertici è un grafico hamiltoniano. Questo segue dalla definizione di grafo completo: un grafo semplice e non diretto tale che ogni coppia di nodi è collegata da un unico bordo.

Il grafo di ogni solido platonico è un grafo hamiltoniano. Così il grafico di un cubo, un tetraedro, un ottaedro o un icosaedro sono tutti grafi hamiltoniani con cicli hamiltoniani.

Un grafico con n vertici (dove n > 3) è hamiltoniano se la somma dei gradi di ogni coppia di vertici non adiacenti è n o maggiore. Questo è noto come teorema di Ore.

Applicazioni dei cicli hamiltoniani e dei grafi

La ricerca di questi cicli non è solo un gioco divertente per il pomeriggio libero. Ha applicazioni reali in campi diversi come la computer grafica, la progettazione di circuiti elettronici, la mappatura dei genomi e la ricerca operativa.

Per esempio, quando si mappano i genomi gli scienziati devono combinare molti piccoli frammenti di codice genetico (“letture”, sono chiamate), in una singola sequenza genomica (una “superstringa”). Questo può essere fatto trovando un percorso o un ciclo hamiltoniano, dove ciascuna delle letture è considerata un nodo in un grafo e ogni sovrapposizione (luogo in cui la fine di una lettura corrisponde all’inizio di un’altra) è considerata un bordo.

In un’applicazione molto meno complessa della stessa matematica, i distretti scolastici usano gli hamiltoniani per pianificare il miglior percorso per prelevare gli studenti da tutto il distretto. Qui gli studenti possono essere considerati nodi, i percorsi tra di loro spigoli, e l’autobus vuole percorrere un percorso che passi esattamente una volta per ogni casa degli studenti.

Gioco di icosi
Su cicli hamiltoniani e percorsi hamiltoniani
Assemblaggio di genomi
Algoritmi grafici in bioinformatica

——————————————————————————

Hai bisogno di aiuto per un compito a casa o per un test? Con Chegg Study, puoi ottenere soluzioni passo dopo passo alle tue domande da un esperto del settore. I tuoi primi 30 minuti con un tutor Chegg sono gratuiti!