グラフ理論 >

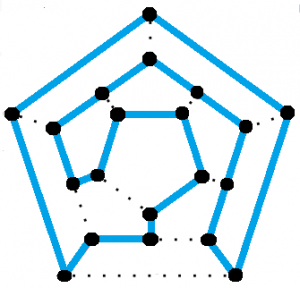
正十二面体（12個の等しい五角形の面を持つ正立体）には、Hamiltonian cycleがあります。

ハミルトニアンサイクルとは、すべてのノード（頂点）がちょうど1回訪れるグラフ上の閉じたループのことです。

ループとは、ノードを自分自身に結合する辺のことで、ハミルトニアンサイクルとは、ある点から自分自身に戻り、途中ですべてのノードを訪れる経路のことです。

複数のノードを持つグラフ(つまり非単調グラフ)がこのタイプのサイクルを持つ場合、それをハミルトニアングラフと呼びます。

グラフがハミルトニアンサイクルを持つかどうかを調べるのに、方程式や一般的なトリックはありません。

ハミルトニアンサイクルの歴史

このサイクルは、1857年にハミルトニアンサイクルを探すパズルゲームを考案したウィリアム・ローワン・ハミルトン卿にちなんで名付けられました。 このゲームは「アイコスゲーム」と呼ばれ、各頂点に穴の開いた正十二面体のグラフとして配布された。 パズルを解き、ゲームに勝つためには、ペグとひもを使ってハミルトンサイクル（すべての穴にちょうど1回ずつ訪れる閉ループ）を見つけなければならない。 その答えは、上の画像に示されています。

ハミルトニアングラフの例

2つ以上の頂点を持つ完全グラフはすべてハミルトニアングラフです。

すべてのPlatonic Solidのグラフはハミルトニアングラフです。

n個の頂点を持つグラフ（n > 3）は、隣接しない頂点のすべてのペアの次数の合計がn以上であればハミルトニアンです。

Applications of Hamiltonian cycles and Graphs

これらのサイクルの探索は、午後の休日の楽しいゲームというだけではありません。

例えば、ゲノムをマッピングする際、科学者は多くの小さな遺伝コードの断片（「リード」と呼ばれる）を1つのゲノム配列（「スーパーストリング」）に結合しなければなりません。 これは、ハミルトンパスまたはサイクルを見つけることによって行うことができます。ここでは、各リードをグラフのノードと見なし、各オーバーラップ（あるリードの終わりと他のリードの始まりが一致する場所）をエッジと見なします。

まったく同じ数学のはるかに複雑でない応用例として、学区では、学区全体から生徒を迎えに行く最適なルートを計画するためにハミルトニアンを使用します。

Icosian Game
On Hamiltonian Cycles and Hamiltonian Paths
Genome Assembly
Graph Algorithms in Bioinformatics

——————————————————————————

宿題やテストの問題で助けが必要ですか？ Chegg Studyでは、その分野の専門家からステップバイステップで質問に対する解決策を得ることができます。 Cheggチューターとの最初の30分は無料です。