Teoría de los gráficos >
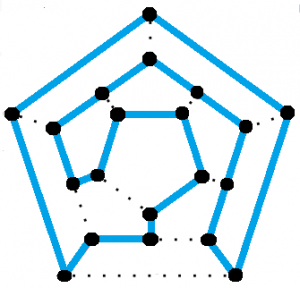
Un dodecaedro ( una figura sólida regular con doce caras pentagonales iguales) tiene un ciclo hamiltoniano.
Un bucle no es más que una arista que une un nodo consigo mismo; por lo que un ciclo hamiltoniano es un camino que viaja desde un punto hasta sí mismo, visitando cada nodo en el camino.
Si un grafo con más de un nodo (es decir, un grafo no solitario) tiene este tipo de ciclo, lo llamamos grafo hamiltoniano.
No hay ninguna ecuación ni truco general para saber si un grafo tiene un ciclo hamiltoniano; la única forma de determinarlo es hacer una búsqueda completa y exhaustiva, recorriendo todas las opciones.
Historia del ciclo hamiltoniano
El ciclo debe su nombre a Sir William Rowan Hamilton, quien, en 1857, inventó un juego de ingenio que consistía en buscar un ciclo hamiltoniano. El juego, llamado juego icosiano, se distribuía como un gráfico dodecaedro con un agujero en cada vértice. Para resolver el rompecabezas o ganar el juego había que utilizar clavijas y cuerdas para encontrar el ciclo hamiltoniano, un bucle cerrado que visitaba cada agujero exactamente una vez. La solución se muestra en la imagen superior.
Ejemplos de grafos hamiltonianos
Todo grafo completo con más de dos vértices es un grafo hamiltoniano. Esto se deduce de la definición de grafo completo: un grafo simple no dirigido tal que cada par de nodos está conectado por una única arista.
El grafo de todo sólido platónico es un grafo hamiltoniano. Así, el grafo de un cubo, un tetraedro, un octaedro o un icosaedro son todos grafos hamiltonianos con ciclos hamiltonianos.
Un grafo con n vértices (donde n > 3) es hamiltoniano si la suma de los grados de cada par de vértices no adyacentes es n o mayor. Esto se conoce como el teorema de Ore.
Aplicaciones de los ciclos hamiltonianos y los grafos
La búsqueda de estos ciclos no es sólo un juego divertido para la tarde libre. Tiene aplicaciones reales en campos tan diversos como los gráficos por ordenador, el diseño de circuitos electrónicos, el mapeo de genomas y la investigación de operaciones.
Por ejemplo, al mapear genomas los científicos deben combinar muchos fragmentos diminutos de código genético («lecturas», se les llama), en una sola secuencia genómica (una «supercadena»). Esto puede hacerse encontrando un camino o ciclo hamiltoniano, en el que cada una de las lecturas se considera un nodo de un grafo y cada solapamiento (lugar en el que el final de una lectura coincide con el principio de otra) se considera una arista.
En una aplicación mucho menos compleja de exactamente las mismas matemáticas, los distritos escolares utilizan Hamiltonians para planificar la mejor ruta para recoger a los estudiantes de todo el distrito. En este caso, los estudiantes pueden considerarse nodos, los caminos entre ellos aristas, y el autobús desea recorrer una ruta que pase por la casa de cada estudiante exactamente una vez.
Juego Icosiano
Sobre Ciclos Hamiltonianos y Caminos Hamiltonianos
Asamblea del Genoma
Algoritmos Gráficos en Bioinformática
Stephanie Glen. «Hamiltonian Cycle: Definición simple y ejemplo» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/hamiltonian-cycle/
——————————————————————————
¿Necesitas ayuda con los deberes o con un examen? Con Chegg Study, puedes obtener soluciones paso a paso a tus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!