Photoelectric Effect
Albert Einstein toonde aan dat de afhankelijkheid van de frequentie niet kon worden gerechtvaardigd door de klassieke golftheorie alleen, dus gaf hij een deeltjesperspectief. In 1905 verklaarde hij dat fotonen (genoemd door G.N. Lewis), “deeltjes van licht” waren die een energie hadden die vergelijkbaar was met die van de vergelijking van Planck. Deze vergelijking stelt dat de frequentie en de energie van een kwantum van elektromagnetische straling evenredig zijn. Einsteins idee was revolutionair omdat hij een nieuw perspectief bracht om licht niet alleen als een golf, maar als een deeltje te zien.
De vergelijking van Planck: E=hv Constante van Planck: h=6,626×10-34 Js 
Het verschijnsel foto-elektrisch effect dat elektronen worden uitgezonden wanneer licht het oppervlak van metalen raakt, werd ontdekt door Heinrich Hertz in 1888. Dit proces gaat op wanneer het invallende licht een hogere frequentie heeft dan een bepaalde drempelwaarde. De hoeveelheid uitgezonden elektronen wordt bepaald door de intensiteit van het invallende licht, maar de frequentie van het licht beïnvloedt de kinetische energieën van de uitgezonden elektronen.
In andere woorden, de intensiteit kan worden omschreven als de helderheid van een lichtbron. Dus als de helderheid toeneemt, neemt de intensiteit toe, en daarmee ook de vrijkomende energie. De afgegeven energie zal groter zijn en wanneer dit gebeurt, neemt de amplitude van de lichtgolf toe. Maar het maakt niet uit hoeveel energie wordt verhoogd of hoeveel je de amplitude verhoogt als het erom gaat te proberen elektronen uit te zenden van een metalen oppervlak. Daarvoor moet de frequentie toenemen.
Verhoogt de helderheid (behoudt frequentie en energie)–>Verhoogt de intensiteit (verhoogt# van fot ons)–>Verhoogt aantal uitgezonden elektronen
ons)–>Verhoogt aantal uitgezonden elektronen
Verhoogt frequentie–>Verhoogt kinetische energie van elektronen
Einstein legde uit dat licht de eigenschap had van een deeltje (foton) met de fotonenergie van E=hv. Hij concludeerde dat als de drempelfrequentie van het metaal groter was dan de frequentie van het foton, het foton geen effect zal hebben wanneer het het metaaloppervlak bombardeert. Als het foton echter de drempelfrequentie bereikt, kan het ervoor zorgen dat één elektron wordt uitgezonden. Om meer elektronen uit te zenden moet de lichtbron helderder worden gemaakt om de intensiteit te verhogen, waardoor de lichtfrequentie en dezelfde energie behouden blijven, maar het aantal fotonen toeneemt.
Drempelfrequentie: Vo= (eVo)/h = werkfunctie/Planck’s constante
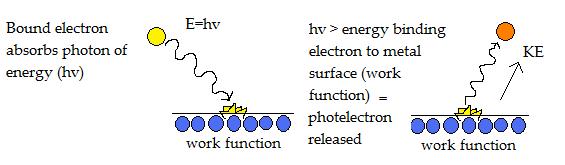
Het foto-elektrisch effect kan zelfs optreden bij de laagste frequentie licht die de drempelfrequentie wordt genoemd.
Photelectronen komen vrij wanneer de fotonenergie (hv) groter is dan de werkfunctie. De overtollige energie komt vrij als kinetische energie in het uitgeworpen foto-elektron en is evenredig met de frequentie van het licht.
Het diagram hierboven illustreert een elektron dat wordt getroffen door een foton met energie, waardoor het de werkfunctie kan overwinnen die het aan het metaaloppervlak bindt. Als gevolg hiervan wordt een foto-elektron met kinetische energie uitgezonden.
Door toepassing van de wet van behoud van energie krijgen we de vergelijking: hv =eVo+(1/2)mv2
Om samen te vatten, ongeacht de intensiteit van het licht, zullen er geen elektronen worden uitgezonden als de frequentie van het licht onder de drempelfrequentie (Vo) van het metaaloppervlak ligt.

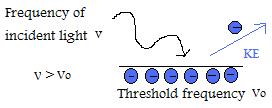
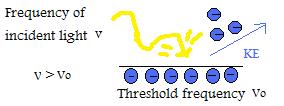
- Als de frequentie van het invallende licht boven de drempelfrequentie ligt, dan zal de kinetische energie van het uitgezonden deeltje lineair toenemen met betrekking tot de grootte van de frequentie.
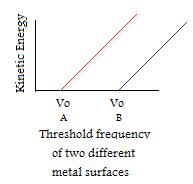
- Als de frequentie van het invallende licht hoger is dan de drempelfrequentie, wordt het aantal geëmitteerde elektronen bepaald door de intensiteit. (BELANGRIJKE OPMERKING: De kinetische energie per elektron verandert niet als de intensiteit wordt veranderd, alleen als de frequentie wordt gemanipuleerd)
- Hoewel elk metaal zijn eigen unieke drempelfrequentie heeft, hebben ze allemaal vergelijkbare patronen.