W rzeczywistym świecie oscylacje rzadko są zgodne z prawdziwym SHM. Pewnego rodzaju tarcie zazwyczaj działa tłumiąco na ruch, tak że zamiera on lub wymaga większej siły, aby go kontynuować. W tym rozdziale przeanalizujemy kilka przykładów tłumionego ruchu harmonicznego i zobaczymy, jak zmodyfikować równania ruchu, by opisać ten bardziej ogólny przypadek.

Struny gitary przestają drgać kilka sekund po ich zerwaniu. Aby nadal huśtać się na huśtawce na placu zabaw, trzeba ją pchać (rysunek). Chociaż często możemy sprawić, że tarcie i inne siły niekonserwatywne są małe lub pomijalne, całkowicie nietłumiony ruch jest rzadkością. W rzeczywistości, możemy nawet chcieć tłumić oscylacje, tak jak w przypadku amortyzatorów samochodowych.

Rysunek \(\) przedstawia masę m przymocowaną do sprężyny o stałej sile k. Masa jest podnoszona do pozycji A0, amplitudy początkowej, a następnie zwalniana. Masa oscyluje wokół położenia równowagi w cieczy o lepkości, ale amplituda maleje przy każdym oscylacji. Dla układu z niewielkim tłumieniem okres i częstotliwość są stałe i prawie takie same jak dla SHM, ale amplituda stopniowo maleje, jak pokazano na rysunku. Dzieje się tak, ponieważ niekonserwatywna siła tłumiąca usuwa energię z układu, zwykle w postaci energii cieplnej.

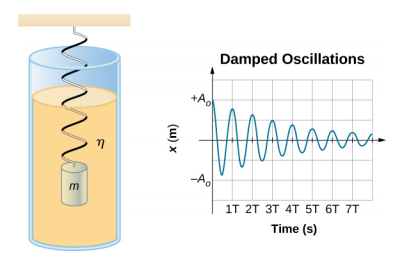
Przemyślmy siły działające na masę. Zauważmy, że jedynym wkładem masy jest zmiana położenia równowagi, co zostało omówione we wcześniejszej części rozdziału. Dlatego siła netto jest równa sile sprężyny i sile tłumienia (F_D). Jeśli wielkość prędkości jest mała, co oznacza, że masa drga powoli, siła tłumiąca jest proporcjonalna do prędkości i działa przeciwnie do kierunku ruchu (\(F_D = -b\)). Siła netto działająca na masę wynosi zatem

Pisząc to jako równanie różniczkowe w x, otrzymujemy

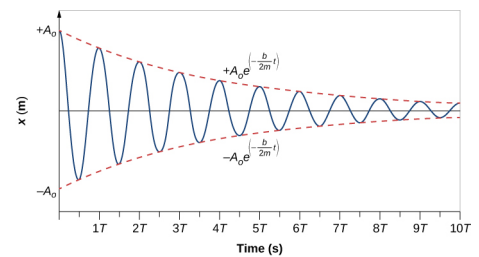
Aby wyznaczyć rozwiązanie tego równania, rozważmy wykres zależności położenia od czasu pokazany na rysunku \(\PageIndex{3}). Krzywa przypomina krzywą kosinusową oscylującą w obwiedni funkcji wykładniczej \(A_0e^{-alfa t}}, gdzie \(\alfa = \frac{b}{2m}}). Rozwiązaniem jest

Zostawiamy jako ćwiczenie udowodnienie, że jest to, w istocie, rozwiązanie. Aby udowodnić, że jest to właściwe rozwiązanie, należy wziąć pierwszą i drugą pochodną względem czasu i podstawić je do równania 15.23. Okazuje się, że równanie 15.24 jest rozwiązaniem, jeżeli

Przypomnijmy, że częstotliwość kątowa masy poddanej SHM jest równa pierwiastkowi kwadratowemu ze stałej siły podzielonej przez masę. Jest to często określane jako naturalna częstotliwość kątowa, która jest przedstawiana jako

Częstotliwość kątowa dla tłumionego ruchu harmonicznego staje się

Przypomnij sobie, że kiedy rozpoczynaliśmy ten opis tłumionego ruchu harmonicznego, stwierdziliśmy, że tłumienie musi być małe. Nasuwają się dwa pytania. Dlaczego tłumienie musi być małe? I jak małe jest małe? Jeśli stopniowo zwiększamy ilość tłumienia w układzie, okres i częstotliwość zaczynają ulegać zmianie, ponieważ tłumienie przeciwstawia się, a więc spowalnia ruch tam i z powrotem. (Siła netto jest mniejsza w obu kierunkach). Jeśli tłumienie jest bardzo duże, układ nawet nie drga – powoli zmierza do równowagi. Częstotliwość kątowa jest równa

Wraz ze wzrostem b, \(\frac{k}{m} – \left(\dfrac{b}{2m}}{right)^{2}} staje się mniejsza i ostatecznie osiąga zero, gdy b = \(\sqrt{4mk}}. Jeśli b staje się większe, to b staje się liczbą ujemną, a b jest liczbą złożoną.

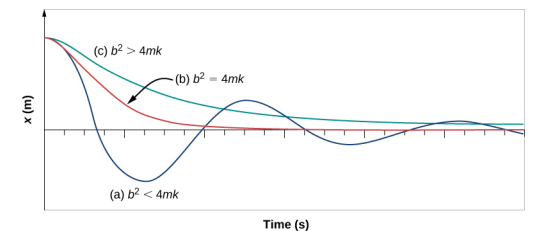
Rysunek \(\) przedstawia przemieszczenie oscylatora harmonicznego dla różnych wartości tłumienia.

1. Gdy stała tłumienia jest mała, b < \(\sqrt{4mk}), układ oscyluje, podczas gdy amplituda ruchu maleje wykładniczo. Mówi się, że taki układ jest niedotłumiony, jak na krzywej (a). Wiele układów jest niedotłumionych i oscyluje, podczas gdy amplituda maleje wykładniczo, np. masa oscylująca na sprężynie. Tłumienie może być dość małe, ale w końcu masa zatrzymuje się.
2. Jeśli stała tłumienia wynosi \(b = \sqrt{4mk}\), mówi się, że system jest krytycznie tłumiony, jak na krzywej (\(b)). Przykładem układu krytycznie tłumionego są amortyzatory w samochodzie. Korzystne jest, aby oscylacje zanikały tak szybko, jak to możliwe. W tym przypadku układ nie oscyluje, ale asymptotycznie zbliża się do stanu równowagi tak szybko, jak to możliwe.
3. Krzywa (c) na rysunku przedstawia układ nadmiernie tłumiony, w którym \(b > \). Układ nadmiernie tłumiony będzie zbliżał się do stanu równowagi w dłuższym okresie czasu.

Tłumienie krytyczne jest często pożądane, ponieważ taki układ szybko wraca do stanu równowagi i również pozostaje w stanie równowagi. Ponadto, stała siła przyłożona do układu krytycznie tłumionego powoduje przesunięcie układu do nowego położenia równowagi w najkrótszym możliwym czasie, bez przesterowania lub oscylacji wokół nowego położenia.