Last Updated on September 25, 2019

Zamiast przewidywać wartości klas bezpośrednio dla problemu klasyfikacji, wygodne może być przewidywanie prawdopodobieństwa przynależności obserwacji do każdej możliwej klasy.

Predicting probabilities allows some flexibility including deciding how to interpret the probabilities, presenting predictions with uncertainty, and providing more nuanced ways to evaluate the skill of the model.

Predicted probabilities that match the expected distribution of probabilities for each class are referred to as calibrated. Problem polega na tym, że nie wszystkie modele uczenia maszynowego są w stanie przewidzieć skalibrowane prawdopodobieństwa.

Istnieją metody pozwalające zarówno zdiagnozować, jak skalibrowane są przewidywane prawdopodobieństwa, jak i lepiej skalibrować przewidywane prawdopodobieństwa z obserwowanym rozkładem każdej klasy. Często może to prowadzić do lepszej jakości przewidywań, w zależności od tego, jak oceniane są umiejętności modelu.

W tym poradniku dowiesz się, jak ważna jest kalibracja przewidywanych prawdopodobieństw oraz jak diagnozować i poprawiać kalibrację modeli używanych do klasyfikacji probabilistycznej.

Po ukończeniu tego kursu będziesz wiedział:

• Nieliniowe algorytmy uczenia maszynowego często przewidują nieskalibrowane prawdopodobieństwa klas.
• Diagramy niezawodności mogą być użyte do zdiagnozowania kalibracji modelu, a metody mogą być użyte do lepszej kalibracji przewidywań dla danego problemu.
• Jak tworzyć diagramy wiarygodności i kalibrować modele klasyfikacyjne w Pythonie za pomocą scikit-learn.

Rozpocznij swój projekt z moją nową książką Probability for Machine Learning, zawierającą tutoriale krok po kroku oraz pliki z kodem źródłowym Pythona dla wszystkich przykładów.

Zacznijmy.

How and When to Use a Calibrated Classification Model with scikit-learn
Photo by Nigel Howe, some rights reserved.

Przegląd samouczka

Tutorial ten podzielony jest na cztery części; są to:

1. Predicting Probabilities
2. Calibration of Predictions
3. How to Calibrate Probabilities in Python
4. Worked Example of Calibrating SVM Probabilities

Predicting Probabilities

Problem modelowania predykcyjnego klasyfikacji wymaga przewidywania lub prognozowania etykiety dla danej obserwacji.

Alternatywą do bezpośredniego przewidywania etykiety może być przewidywanie prawdopodobieństwa przynależności obserwacji do każdej możliwej etykiety klasy.

Daje to pewną elastyczność zarówno w sposobie interpretacji i prezentacji przewidywań (wybór progu i niepewności przewidywań), jak i w sposobie oceny modelu.

Mimo, że model może być w stanie przewidywać prawdopodobieństwa, rozkład i zachowanie prawdopodobieństw może nie odpowiadać oczekiwanemu rozkładowi prawdopodobieństw obserwowanych w danych treningowych.

Jest to szczególnie częste w przypadku złożonych nieliniowych algorytmów uczenia maszynowego, które nie dokonują bezpośrednio przewidywań probabilistycznych, a zamiast tego wykorzystują przybliżenia.

Rozkład prawdopodobieństw można dostosować, aby lepiej odpowiadał oczekiwanemu rozkładowi zaobserwowanemu w danych. To dostosowanie jest określane jako kalibracja, tak jak w przypadku kalibracji modelu lub kalibracji rozkładu prawdopodobieństw klas.

Chcemy, aby oszacowane prawdopodobieństwa klas odzwierciedlały prawdziwe prawdopodobieństwo leżące u podstaw próbki. Oznacza to, że przewidywane prawdopodobieństwo klasy (lub wartość podobna do prawdopodobieństwa) musi być dobrze skalibrowane. Aby być dobrze skalibrowanym, prawdopodobieństwa muszą efektywnie odzwierciedlać prawdziwe prawdopodobieństwo zdarzenia będącego przedmiotem zainteresowania.

– Strona 249, Applied Predictive Modeling, 2013.

Kalibracja przewidywań

W kalibracji prawdopodobieństw występują dwa problemy; są to diagnozowanie kalibracji przewidywanych prawdopodobieństw oraz sam proces kalibracji.

Diagramy niezawodności (krzywe kalibracji)

Diagram niezawodności jest wykresem liniowym względnej częstości tego, co zostało zaobserwowane (oś y) w stosunku do przewidywanej częstości prawdopodobieństwa (oś x).

Diagramy niezawodności są powszechnym narzędziem do ilustracji właściwości systemów prognoz probabilistycznych. Składają się one z wykresu obserwowanej częstotliwości względnej względem przewidywanego prawdopodobieństwa, zapewniając szybkie wizualne porównanie podczas dostrajania probabilistycznych systemów prognostycznych, jak również dokumentując wydajność produktu końcowego

– Increasing the Reliability of Reliability Diagrams, 2007.

Specyficznie, przewidywane prawdopodobieństwa są podzielone na stałą liczbę kubełków wzdłuż osi x. Liczba zdarzeń (class=1) jest następnie zliczana dla każdego przedziału (np. względna obserwowana częstość). Na koniec zliczenia są normalizowane. Wyniki są następnie wykreślane jako wykres liniowy.

W literaturze prognostycznej wykresy te są powszechnie określane jako wykresy „niezawodności”, chociaż mogą być również nazywane wykresami „kalibracyjnymi” lub krzywymi, ponieważ podsumowują one, jak dobrze prawdopodobieństwa prognozy są skalibrowane.

Im lepiej skalibrowana lub bardziej wiarygodna prognoza, tym bliżej punkty pojawią się wzdłuż głównej przekątnej od dołu po lewej do góry po prawej stronie wykresu.

Położenie punktów lub krzywej względem przekątnej może pomóc w interpretacji prawdopodobieństwa; na przykład:

• Poniżej przekątnej: Model zawyżył prognozę; prawdopodobieństwa są zbyt duże.
• Powyżej przekątnej: Model ma zaniżoną prognozę; prawdopodobieństwa są zbyt małe.

Prawdopodobieństwa, z definicji, są ciągłe, więc oczekujemy pewnego oddzielenia od linii, często pokazywanej jako krzywa w kształcie litery S, pokazująca pesymistyczne tendencje do zawyżania prognozy przy niskich prawdopodobieństwach i zaniżania prognozy przy wysokich prawdopodobieństwach.

Diagramy wiarygodności zapewniają diagnostykę w celu sprawdzenia, czy prognozowana wartość Xi jest wiarygodna. Z grubsza rzecz ujmując, prognoza prawdopodobieństwa jest wiarygodna, jeśli zdarzenie faktycznie ma miejsce z obserwowaną względną częstością zgodną z wartością prognozy.

– Increasing the Reliability of Reliability Diagrams, 2007.

Diagram wiarygodności może pomóc zrozumieć względną kalibrację prognoz z różnych modeli predykcyjnych.

Kalibracja prawdopodobieństwa

Prognozy wykonane przez model predykcyjny mogą być kalibrowane.

Skalibrowane przewidywania mogą (lub nie) skutkować poprawioną kalibracją na wykresie wiarygodności.

Niektóre algorytmy są dopasowane w taki sposób, że ich przewidywane prawdopodobieństwa są już skalibrowane. Nie wdając się w szczegóły, regresja logistyczna jest jednym z takich przykładów.

Inne algorytmy nie dają bezpośrednio przewidywań prawdopodobieństwa, a zamiast tego przewidywanie prawdopodobieństwa musi być przybliżone. Niektóre przykłady obejmują sieci neuronowe, maszyny wektorów nośnych i drzewa decyzyjne.

Przewidywane prawdopodobieństwa z tych metod będą prawdopodobnie nieskalibrowane i mogą skorzystać z modyfikacji poprzez kalibrację.

Kalibracja prawdopodobieństw predykcji jest operacją przeskalowania, która jest stosowana po wykonaniu predykcji przez model predykcyjny.

Istnieją dwa popularne podejścia do kalibracji prawdopodobieństw; są to Skalowanie Platt’a i Regresja Izotoniczna.

Skalowanie Platt’a jest prostsze i nadaje się do diagramów niezawodności o kształcie litery S. Skalowanie Platt’a jest bardziej złożone. Regresja izotoniczna jest bardziej złożona, wymaga znacznie większej ilości danych (w przeciwnym razie może być niedopasowana), ale może obsługiwać wykresy niezawodności o różnych kształtach (jest nieparametryczna).

Skalowanie Platta jest najbardziej efektywne, gdy zniekształcenie przewidywanych prawdopodobieństw ma kształt sigmoidy. Regresja izotoniczna jest bardziej wydajną metodą kalibracji, która może skorygować każde monotoniczne zniekształcenie. Niestety, ta dodatkowa moc ma swoją cenę. Analiza krzywej uczenia pokazuje, że Regresja Izotoniczna jest bardziej podatna na przepasowanie, a zatem działa gorzej niż Skalowanie Platt’a, gdy danych jest mało.

– Predicting Good Probabilities With Supervised Learning, 2005.

Uwaga, i to jest naprawdę ważne: lepiej skalibrowane prawdopodobieństwa mogą lub nie mogą prowadzić do lepszych przewidywań opartych na klasach lub prawdopodobieństwach. To naprawdę zależy od konkretnej metryki używanej do oceny przewidywań.

W rzeczywistości, niektóre wyniki empiryczne sugerują, że algorytmy, które mogą odnieść większe korzyści z kalibracji przewidywanych prawdopodobieństw to SVM, drzewa decyzyjne z workiem i lasy losowe.

po kalibracji najlepszymi metodami są drzewa boostowane, lasy losowe i SVM.

– Predicting Good Probabilities With Supervised Learning, 2005.

How to Calibrate Probabilities in Python

Biblioteka uczenia maszynowego scikit-learn pozwala zarówno zdiagnozować kalibrację prawdopodobieństwa klasyfikatora, jak i skalibrować klasyfikator, który może przewidywać prawdopodobieństwa.

Diagnostyka kalibracji

Możesz zdiagnozować kalibrację klasyfikatora poprzez stworzenie wykresu wiarygodności rzeczywistych prawdopodobieństw w stosunku do przewidywanych prawdopodobieństw na zbiorze testowym.

W scikit-learn nazywa się to krzywą kalibracji.

Można to zaimplementować poprzez obliczenie funkcji calibration_curve(). Funkcja ta pobiera prawdziwe wartości klas dla zbioru danych i przewidywane prawdopodobieństwa dla klasy głównej (class=1). Funkcja zwraca prawdziwe prawdopodobieństwa dla każdego bloku i przewidywane prawdopodobieństwa dla każdego bloku. Liczba bloków może być określona poprzez argument n_bins i domyślnie wynosi 5.

Na przykład, poniżej znajduje się wycinek kodu pokazujący użycie API:

Kalibracja klasyfikatora

Klasyfikator można skalibrować w scikit-learn za pomocą klasy CalibratedClassifierCV.

Istnieją dwa sposoby użycia tej klasy: prefit i walidacja krzyżowa.

Można dopasować model na zbiorze danych treningowych i skalibrować ten model prefit używając zbioru danych walidacyjnych.

Na przykład, poniżej znajduje się fragment kodu pokazujący użycie API:

1 2 3 4 5 6 7 8 9 10 11 12 13

… # prepare data trainX, trainy = … valX, valy = … testX, testiny = … # fit base model on training dataset model = … model.fit(trainX, trainy) # kalibruj model na danych walidacyjnych calibrator = CalibratedClassifierCV(model, cv=’prefit') calibrator.fit(valX, valy) # oceń model yhat = calibrator.predict(testX)

Alternatywnie, CalibratedClassifierCV może dopasować wiele kopii modelu przy użyciu k-krotnej walidacji krzyżowej i skalibrować prawdopodobieństwa przewidywane przez te modele przy użyciu zestawu hold out. Przewidywania są wykonywane przy użyciu każdego z wytrenowanych modeli.

Na przykład, poniżej znajduje się wycinek kodu pokazujący użycie API:

1 2 3 4 5 6 7 8 9 10 11

… # prepare data trainX, trainy = … testX, testy = … # define base model model = … # dopasować i skalibrować model na danych treningowych calibrator = CalibratedClassifierCV(model, cv=3) calibrator.fit(trainX, trainy) # ocenić model yhat = calibrator.predict(testX)

Klasa CalibratedClassifierCV obsługuje dwa rodzaje kalibracji prawdopodobieństwa; konkretnie parametryczną metodę „sigmoidalną” (metoda Platta) oraz nieparametryczną metodę „izotoniczną”, którą można określić za pomocą argumentu „method”.

Pracowy przykład kalibracji prawdopodobieństwa SVM

Możemy skonkretyzować dyskusję o kalibracji za pomocą kilku przykładów.

W tych przykładach, dopasujemy maszynę wektorów podporowych (SVM) do hałaśliwego problemu klasyfikacji binarnej i użyjemy modelu do przewidywania prawdopodobieństw, a następnie przejrzymy kalibrację używając diagramu wiarygodności i skalibrujemy klasyfikator oraz przejrzymy wynik.

SVM jest dobrym kandydatem na model do kalibracji, ponieważ nie przewiduje on natywnie prawdopodobieństw, co oznacza, że prawdopodobieństwa są często nieskalibrowane.

Uwaga na temat SVM: prawdopodobieństwa mogą być przewidywane przez wywołanie funkcji decision_function() na dopasowanym modelu zamiast zwykłej funkcji predict_proba(). Prawdopodobieństwa nie są znormalizowane, ale mogą być znormalizowane podczas wywoływania funkcji calibration_curve() poprzez ustawienie argumentu 'normalize' na 'True'.

Poniższy przykład dopasowuje model SVM do problemu testowego, przewiduje prawdopodobieństwa i wykreśla kalibrację prawdopodobieństw w postaci wykresu wiarygodności,

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22

# SVM diagram wiarygodności from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # podziel na zestawy train/test trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # fit a model model = SVC() model.fit(trainX, trainy) # predict probabilities probs = model.decision_function(testX) # wykres wiarygodności fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfectly calibrated pyplot.plot(, , linestyle='–') # plot model reliability pyplot.plot(mpv, fop, marker='.') pyplot.show()

Wykonanie przykładu tworzy wykres wiarygodności pokazujący kalibrację SVM-ów przewidywanych prawdopodobieństw (linia ciągła) w porównaniu do idealnie skalibrowanego modelu wzdłuż przekątnej wykresu (linia przerywana.Widzimy oczekiwaną krzywą w kształcie litery S konserwatywnej prognozy.

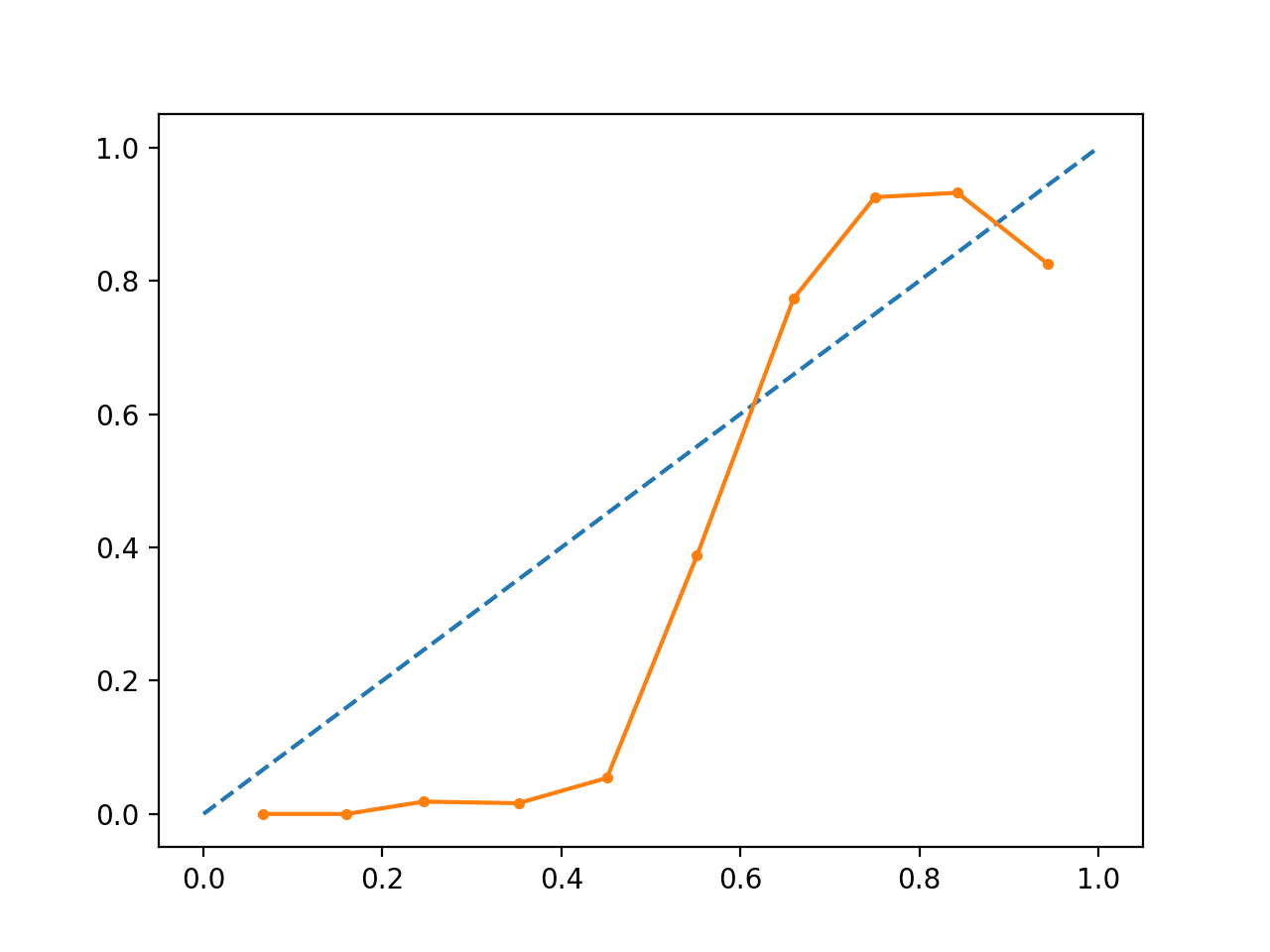
Wykres wiarygodności nieskalibrowanego SVM

Możemy zaktualizować przykład, aby dopasować SVM poprzez klasę CalibratedClassifierCV używając 5-krotnej walidacji krzyżowej, używając zbiorów holdout do kalibracji przewidywanych prawdopodobieństw.

Pełny przykład znajduje się poniżej.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24

# Wykres wiarygodności SVM z kalibracją from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # podziel na zbiory train/test trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # fit a model model = SVC() calibrated = CalibratedClassifierCV(model, method=’sigmoid', cv=5) calibrated.fit(trainX, trainy) # predict probabilities probs = calibrated.predict_proba(testX) # wykres wiarygodności fop, mpv = calibration_curve(testy, probs, n_bins=10, normalize=True) # plot perfectly calibrated pyplot.plot(, , linestyle='–') # plot wiarygodność skalibrowana pyplot.plot(mpv, fop, marker='.') pyplot.show()

Wykonanie przykładu tworzy wykres wiarygodności dla skalibrowanych prawdopodobieństw.

Kształt skalibrowanych prawdopodobieństw jest inny, znacznie lepiej przylega do linii ukośnej, chociaż nadal nie przewiduje się prognoz w górnym kwadrancie.

Wyraźnie widać, że wykres sugeruje lepiej skalibrowany model.

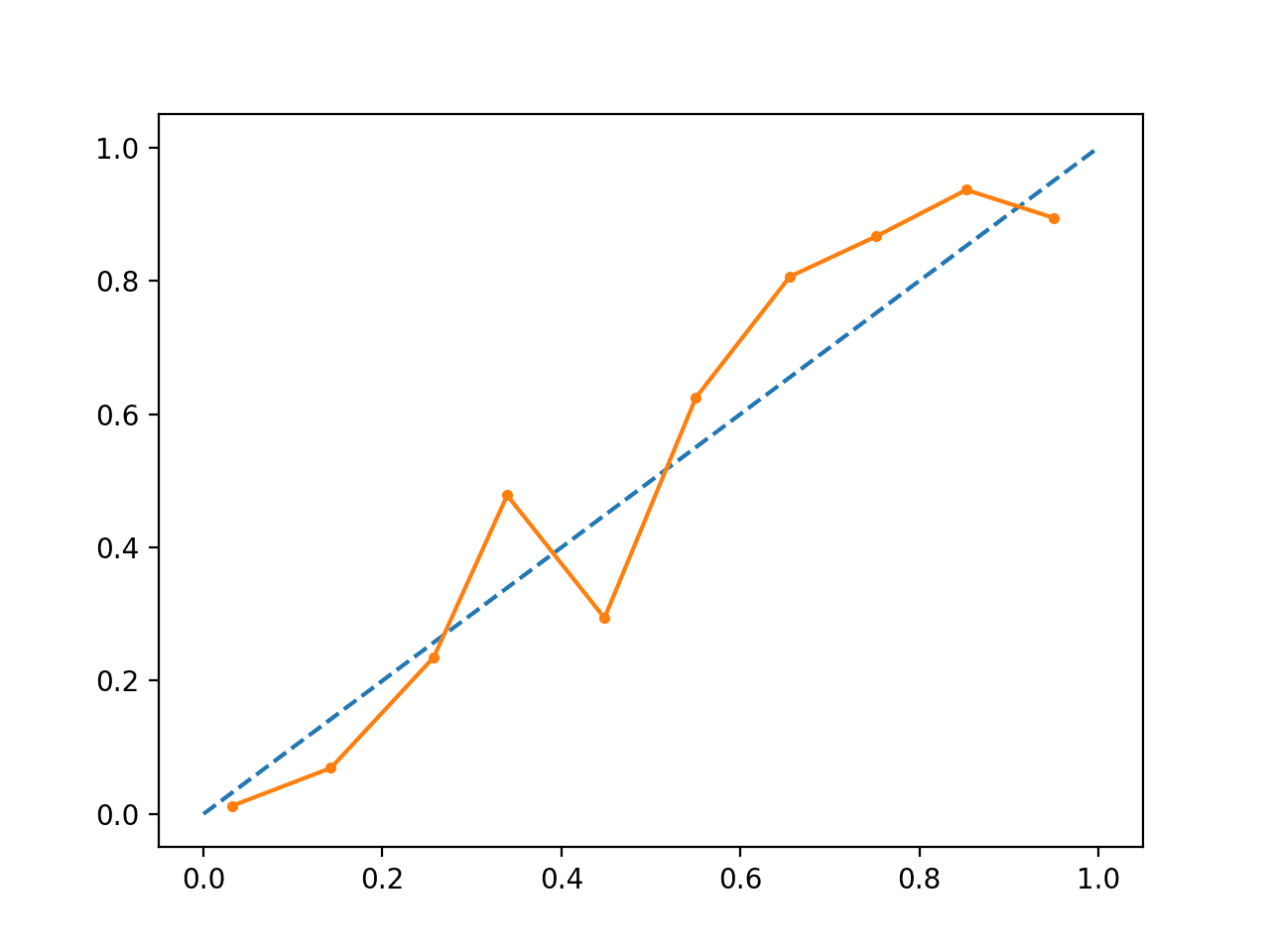
Skalibrowany wykres wiarygodności SVM

Możemy uczynić kontrast między dwoma modelami bardziej oczywistym, umieszczając oba wykresy wiarygodności na tym samym wykresie.

Pełny przykład znajduje się poniżej.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43

# Wykresy wiarygodności SVM z nieskalibrowanymi i skalibrowanymi prawdopodobieństwami from sklearn.datasets import make_classification from sklearn.svm import SVC from sklearn.calibration import CalibratedClassifierCV from sklearn.model_selection import train_test_split from sklearn.calibration import calibration_curve from matplotlib import pyplot # predict uncalibrated probabilities def uncalibrated(trainX, testX, trainy): # fit a model model = SVC() model.fit(trainX, trainy) # predict probabilities return model.decision_function(testX) # predict calibrated probabilities def calibrated(trainX, testX, trainy): # zdefiniuj model model = SVC() # zdefiniuj i dopasuj model kalibracyjny calibrated = CalibratedClassifierCV(model, method=’sigmoid', cv=5) calibrated.fit(trainX, trainy) # predict probabilities return calibrated.predict_proba(testX) # generate 2 class dataset X, y = make_classification(n_samples=1000, n_classes=2, weights=, random_state=1) # split into train/test sets trainX, testX, trainy, testy = train_test_split(X, y, test_size=0.5, random_state=2) # nieskalibrowane predykcje yhat_uncalibrated = uncalibrated(trainX, testX, trainy) # predictions calibrated yhat_calibrated = calibrated(trainX, testX, trainy) # diagramy wiarygodności fop_uncalibrated, mpv_uncalibrated = calibration_curve(testy, yhat_uncalibrated, n_bins=10, normalize=True) fop_calibrated, mpv_calibrated = calibration_curve(testy, yhat_calibrated, n_bins=10) # plot perfectly calibrated pyplot.plot(, , linestyle='–', color=’black') # plot model reliability pyplot.plot(mpv_uncalibrated, fop_uncalibrated, marker='.') pyplot.plot(mpv_calibrated, fop_calibrated, marker='.') pyplot.show()

Uruchomienie przykładu tworzy pojedynczy wykres wiarygodności pokazujący zarówno skalibrowane (pomarańczowe), jak i nieskalibrowane (niebieskie) prawdopodobieństwa.

Nie jest to tak naprawdę porównanie jabłek do jabłek, ponieważ przewidywania dokonane przez skalibrowany model są w rzeczywistości kombinacją pięciu podmodeli.

Niemniej jednak, widzimy wyraźną różnicę w wiarygodności skalibrowanych prawdopodobieństw (bardzo prawdopodobnie spowodowaną procesem kalibracji).

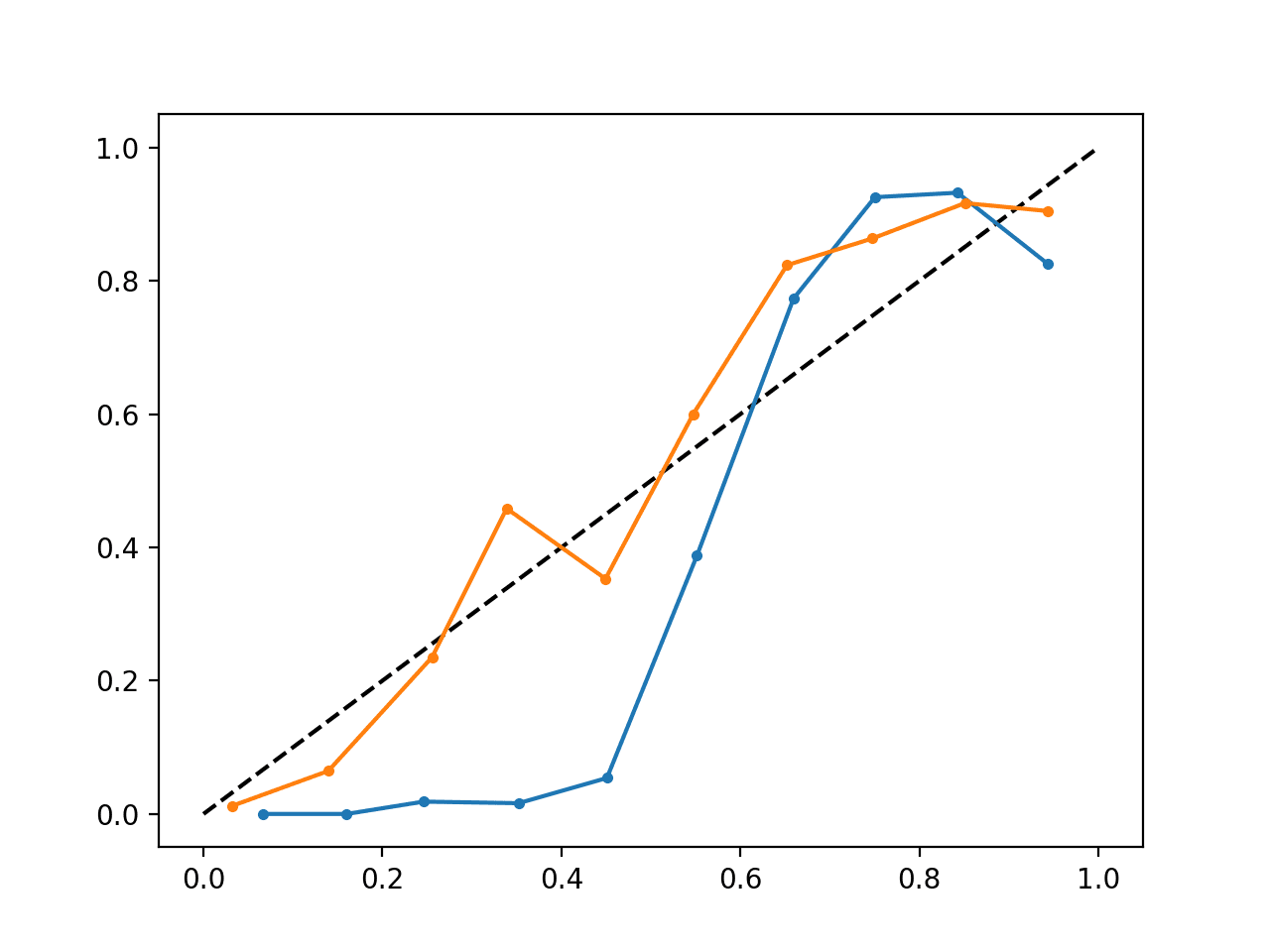
Skalibrowany i nieskalibrowany wykres wiarygodności SVM

Dalsza lektura

Ta sekcja zawiera więcej zasobów na ten temat, jeśli chcesz się zagłębić.

Books and Papers

• Applied Predictive Modeling, 2013.
• Predicting Good Probabilities With Supervised Learning, 2005.
• Obtaining calibrated probability estimates from decision trees and naive Bayesian classifiers, 2001.
• Increasing the Reliability of Reliability Diagrams, 2007.

API

• sklearn.calibration.CalibratedClassifierCV API
• sklearn.calibration.calibration_curve API
• Kalibracja prawdopodobieństwa, scikit-learn User Guide
• Krzywe kalibracji prawdopodobieństwa, scikit-learn
• Porównanie kalibracji klasyfikatorów, scikit-learn

Artykuły

• Strona weryfikacji CAWCAR
• Kalibracja (statystyka) w Wikipedii
• Klasyfikacja probabilistyczna w Wikipedii
• Klasyfikacja probabilistyczna na Wikipedii
• Scikit poprawny sposób kalibracji klasyfikatorów z CalibratedClassifierCV na CrossValidated

Podsumowanie

W tym tutorialu, dowiedziałeś się jak ważna jest kalibracja przewidywanych prawdopodobieństw oraz jak diagnozować i poprawiać kalibrację modeli używanych do klasyfikacji probabilistycznej.

Szczegółowo, dowiedziałeś się:

• Nieliniowe algorytmy uczenia maszynowego często przewidują nieskalibrowane prawdopodobieństwa klas.
• Diagramy niezawodności mogą być użyte do zdiagnozowania kalibracji modelu, a metody mogą być użyte do lepszej kalibracji przewidywań dla danego problemu.
• Jak tworzyć diagramy wiarygodności i kalibrować modele klasyfikacyjne w Pythonie za pomocą scikit-learn.

Masz jakieś pytania?
Pytaj w komentarzach poniżej, a ja postaram się odpowiedzieć.

Zdobądź wskazówki na temat prawdopodobieństwa dla uczenia maszynowego!

Rozwiń swoje zrozumienie prawdopodobieństwa

….z zaledwie kilkoma liniami kodu Pythona

Odkryj, jak to zrobić w moim nowym podręczniku:
Probability for Machine Learning

Zawiera on samouczki i projekty typu end-to-end na temat:
Twierdzenia Bayesa, optymalizacji bayesowskiej, rozkładów, maksymalnej wiarygodności, entropii krzyżowej, kalibracji modeli
i wiele więcej…

Wreszcie ujarzmij niepewność w swoich projektach

Opuść akademickość. Po prostu Wyniki.Zobacz, Co Jest Wewnątrz

Tweetuj Udostępnij Udostępnij