Familywise Error Rates > Metoda Holma-Metoda Bonferroniego

Możesz najpierw przeczytać ten artykuł: Familywise Error Rates.

Co to jest Metoda Holma-Bonferroniego?

Metoda Holma-Bonferroniego (zwana również Sekwencyjną Procedurą Bonferroniego Holma) jest sposobem radzenia sobie z rodzinnymi współczynnikami błędu (FWER) dla wielokrotnych testów hipotez. Jest ona modyfikacją korekty Bonferroniego. Korekta Bonferroniego zmniejsza możliwość uzyskania statystycznie istotnego wyniku (tj. błędu typu I) podczas wykonywania testów wielokrotnych. Chociaż Bonferroniego jest prosta do obliczenia, to cierpi na brak mocy statystycznej. Metoda Holm-Bonferroni jest również dość prosta do obliczenia, ale jest bardziej wydajna niż jednoetapowy Bonferroni.

Formuła

Wzór do obliczenia Holm-Bonferroni to: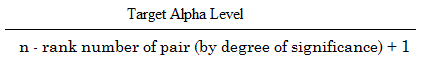

Gdzie:

• Docelowy poziom alfa = ogólny poziom alfa (zwykle .05),
• n = liczba testów.

Kolejny przykład pokazuje jak działa ta formuła.

Przykład

Pytanie: Użyj metody Holma-Bonferroniego, aby przetestować następujące cztery hipotezy i związane z nimi wartości p przy poziomie alfa równym .05:

• H1 = 0.01.
• H2 = 0.04
• H3 = 0.03
• H4 = 0.005

Uwaga: znamy już wartości p związane z każdą hipotezą. Jeśli nie znasz wartości p, przeprowadź test dla każdej hipotezy przed próbą skorygowania FWER metodą Holma-Bonferroniego.

Krok 1: Uporządkuj wartości p od najmniejszej do największej:

• H4 = 0.005
• H1 = 0,01
• H3 = 0,03
• H2 = 0,04

Krok 2: Wyprowadź wzór Holma-Bonferroniego dla pierwszego rzędu:
HB = Cel α / (n – ranga + 1)
HB = .05 / 4 – 1 + 1 = .05 / 4 = .0125.

Krok 3: Porównaj pierwszorzędną (najmniejszą) wartość p z Kroku 1 z poziomem alfa obliczonym w Kroku 2:
Najmniejsza wartość p, w Kroku 1 (H4 = 0.005) < Poziom alfa w Kroku 2 (.0125).
Jeśli wartość p jest mniejsza, odrzuć hipotezę zerową dla tego testu indywidualnego.

Wartość p równa .005 jest mniejsza niż .0125, więc hipoteza zerowa dla H4 zostaje odrzucona.

Krok 4: Powtórz wzór HB dla drugiego rzędu .
HB = Cel α / (n – ranga + 1)
HB = .05 / 4 – 2 + 1 = .05 / 3 = .0167

Krok 5: Porównaj wynik ze wzoru HB w kroku 4 z wartością p drugiego rzędu:
Wartość p drugiej rangi, w kroku 1 (H1 = 0,01) < Poziom alfa w kroku 2 (.0167).
Wartość p równa .01 jest mniejsza niż .0167, więc hipoteza zerowa dla H1 jest również odrzucona.

Krok 6: Powtórz wzór HB dla trzeciej rangi.
HB = Cel α / (n – ranga + 1)
HB = .05 / 4 – 3 + 1 = .05 / 2 = .025

Krok 7: Porównaj wynik z wzoru HB w kroku 6 z wartością p trzeciej rangi:
Wartość p trzeciej rangi, w kroku 1 (H3 = 0,03) > Poziom alfa w kroku 6 (.025).
Wartość p .03 jest większa niż .025, więc hipoteza zerowa dla H3 nie jest odrzucona.

Testowanie zatrzymuje się po osiągnięciu pierwszej nieodrzuconej hipotezy. Wszystkie kolejne hipotezy są nieistotne (tzn. nie odrzucone).

Referencja:
Holm, S. 1979. A simple sequential rejective multiple test procedure. Scandinavian Journal of Statistics 6:65-70

——————————————————————————

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!