قانون برافي (Ar). Loi de Bragg (Fr). Bragg-Gesetz (Ge). Legge di Bragg (It). ブラッグの法則 (Ja). Условие Вульфа – Брэгга (Ru). Ley de Bragg (Sp).

Definicja

Praworagga określa warunek dyfrakcji fali płaskiej przez rodzinę płaszczyzn kratowych:

2 d sin θ = n λ

gdzie d jest odstępem międzypłaszczyznowym, θ kątem między wektorem falowym padającej fali płaskiej, ko, a płaszczyznami kratowymi, λ jej długością fali, a n jest liczbą całkowitą, rzędem odbicia. Jest to równoważne warunkowi dyfrakcji w przestrzeni wzajemnej i równaniom Lauego.

Pośrednie wyprowadzenie prawa Bragga

• Odbicie od pierwszej płaszczyzny

Fale rozproszone będą w fazie niezależnie od rozkładu punktowych rozpraszaczy w pierwszej płaszczyźnie, jeśli kąt wektora fali odbitej, kh, jest również równy θ. Jest to prawo odbicia Snella-Descartesa.

• Odbicie od drugiej płaszczyzny

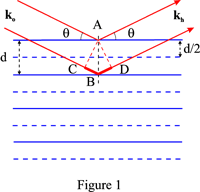
Ponieważ faza fal odbitych jest niezależna od położenia rozpraszacza punktowego na płaszczyźnie, różnicę faz między falami odbitymi od dwóch kolejnych płaszczyzn kratowych otrzymamy wybierając arbitralnie punkt rozpraszania, A, na pierwszej płaszczyźnie i punkt rozpraszania, B, na drugiej płaszczyźnie, tak że AB jest normalny do płaszczyzn. Jeżeli C i D są rzutami punktu A na wektory fal padających i odbitych przechodzących przez punkt B, to z rysunku 1 wynika, że różnica dróg pomiędzy falami odbitymi odpowiednio w punkcie A i B wynosi:

CB + BD = 2d sin θ

oraz że obie fale będą w fazie, jeśli ta różnica ścieżek będzie równa nλ, gdzie n jest liczbą całkowitą.

• Odbicie od trzeciej, itd. płaszczyzn

Jeśli relacja Bragga jest spełniona dla dwóch pierwszych płaszczyzn, to fale odbite z wektorem falowym kh będą w fazie dla wszystkich płaszczyzn z rodziny.

Order odbicia

Prawo Bragga można również zapisać:

2 (d/n) sin θ = λ.

Można więc powiedzieć, że odbicie Bragga rzędu n na rodzinie płaszczyzn kratowych rzędu n jest równoważne odbiciu rzędu 1 na rodzinie fikcyjnych, czyli urojonych, płaszczyzn o odstępach kratowych

d_{hkl} = d/n.

Ta fikcyjna rodzina jest związana z odwrotnym wektorem sieciowym OH, gdzie OH = n/d = 1/d_{hkl}. Indeksy odbicia są równe hkl. Na przykład, przerywane linie poziome na rysunku 1 odpowiadają fikcyjnym płaszczyznom związanym z drugim rzędem, n = 2.

Warunki odbicia

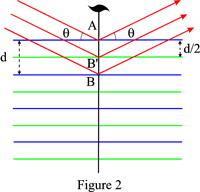
Jeśli istnieje płaszczyzna ślizgowa lub oś śrubowa normalna do płaszczyzn sieci, to odstęp rzeczywistych płaszczyzn odbijających wynosi d/2 dla płaszczyzny ślizgowej i (d p/q) dla osi śrubowej qp. Prawo Bragga należy więc zapisać następująco:

2 (d/2) sin θ = n λ ⇒ 2 d sin θ = 2n λ

dla płaszczyzny ślizgowej i

.

2 (d p/q) sin θ = n λ ⇒ 2 d sin θ = (q/p)n λ

dla osi śrubowej qp.

Odbicia nieparzystego rzędu dla płaszczyzny ślizgowej i rzędu innego niż (q/p)n dla osi śrubowej są wtedy nieobecne. Mówi się o systematycznych nieobecnościach związanych z obecnością składowych ślizgowych lub śrubowych.

Jako przykład na rysunku 2 pokazano przypadek osi 21 śrubowej: płaszczyznami odbijającymi są płaszczyzny niebieskie i płaszczyzny zielone wydedukowane z tych ostatnich przez działanie osi śrubowej. Odbicia nieparzystego rzędu będą systematycznie nieobecne.

Wpływ deformacji

Odkształcenie, które pozostawia rodzinę płaszczyzn sieciowych (hkl) niezniekształconą, a jej odstępy sieciowe d niezmienione, nie będzie miało wpływu na kąt Bragga odbić kkl, np.np. płaszczyzny równoległe do dyslokacji śrubowych.

Historia

Bragg (1890-1971) przedstawił swoje wyprowadzenie warunku odbicia na spotkaniu Cambridge Philosophical Society 11 listopada 1912 roku. Jego praca została opublikowana w 1913 roku. Szczegóły, patrz P. P. Ewald (1962), 50 Years of X-ray Diffraction, Utrecht: IUCr/Oosthoek, Section 5, s. 64 i A. Authier (2013), The Early Days of X-ray Diffraction, Oxford: IUCr/Oxford University Press, Section 6.11, s. 120.

Zobacz także

• Równania Laue