To jest wektor:

Wektor ma wielkość (rozmiar) i kierunek:
Długość linii pokazuje jej wielkość, a grot strzałki wskazuje kierunek.
Dwa wektory możemy dodać, łącząc je od stóp do głów:
I nie ma znaczenia, w jakiej kolejności je dodamy, otrzymamy ten sam wynik:
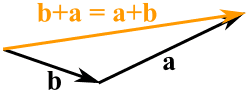
Przykład: Samolot leci wzdłuż, kierując się na północ, ale wieje wiatr z północnego zachodu.
Dwa wektory (prędkość spowodowana przez śmigło oraz prędkość wiatru) powodują, że samolot ma nieco mniejszą prędkość względem ziemi, kierując się nieco na wschód od północy.
Gdybyś obserwował samolot z ziemi, wydawałoby się, że trochę się ślizga na boki.
Czy kiedykolwiek widziałeś, że tak się dzieje? Może widziałeś ptaki walczące z silnym wiatrem, które wydają się lecieć na boki. Wektory pomagają to wyjaśnić.
Prędkość, przyspieszenie, siła i wiele innych rzeczy są wektorami.
Odejmowanie
Możemy również odjąć jeden wektor od drugiego:
- Najpierw odwracamy kierunek wektora, który chcemy odjąć,
- potem dodajemy je jak zwykle:
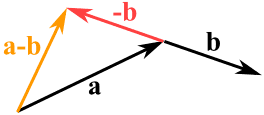
a – b
Notacja
Wektor często jest pisany pogrubioną czcionką, jak a lub b.
| Wektor można też zapisać jako litery jego głowy i ogona ze strzałką nad nimi, jak poniżej: |
 |
Obliczenia
Teraz …. w jaki sposób wykonujemy obliczenia?
Najczęstszym sposobem jest najpierw rozbicie wektorów na części x i y, jak poniżej:
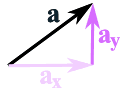
Wektor a jest rozbity na
dwa wektory ax i ay
(Zobaczymy później jak to zrobić.)
Dodawanie wektorów
Możemy wtedy dodawać wektory przez dodawanie części x i dodawanie części y:
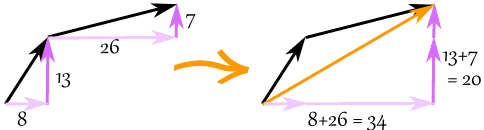
Wektor (8, 13) i wektor (26, 7) dodają się do wektora (34, 20)
Przykład: dodajemy wektory a = (8, 13) i b = (26, 7)
c = a + b
c = (8, 13) + (26, 7) = (8+26, 13+7) = (34, 20)
Gdy tak rozbijamy wektor, każdą część nazywamy składową:
Odejmowanie wektorów
Aby odjąć, najpierw odwróć wektor, który chcemy odjąć, a następnie dodaj.
Przykład: odejmujemy k = (4, 5) od v = (12, 2)
a = v + -k
a = (12, 2) + -(4, 5) = (12, 2) + (-4, -5) = (12-4, 2-5) = (8, -3)
Magnitude of a Vector
Magnitude of a vector is shown by two vertical bars on either side of the vector:
|a|
Albo może być zapisana z podwójnymi pionowymi kreskami (aby nie pomylić jej z wartością bezwzględną):
|a|
Wykorzystujemy twierdzenie Pitagorasa, aby ją obliczyć:
|a| = √( x2 + y2 )
Przykład: jaka jest wielkość wektora b = (6, 8) ?
|b| = √( 62 + 82) = √( 36+64) = √100 = 10
Wektor o wielkości 1 nazywamy wektorem jednostkowym.
Wektor vs skalar
Skalar ma tylko wielkość (rozmiar).
Skalar: po prostu liczba (jak 7 lub -0,32) … zdecydowanie nie jest wektorem.
Wektor ma wielkość i kierunek, i jest często pisany pogrubioną czcionką, więc wiemy, że nie jest skalarem:
- więc c jest wektorem, ma wielkość i kierunek
- ale c jest tylko wartością, jak 3 lub 12.4
Przykład: kb jest w rzeczywistości skalarem k razy wektor b.
Mnożenie wektora przez skalar
Gdy mnożymy wektor przez skalar, nazywamy to „skalowaniem” wektora, ponieważ zmieniamy jak duży lub mały jest wektor.
Przykład: mnożymy wektor m = (7, 3) przez skalar 3
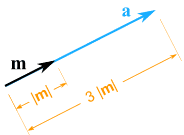 |
a = 3m = (3×7, 3×3) = (21, 9) |
Wciąż wskazuje w tym samym kierunku, ale jest 3 razy dłuższy
(I teraz wiesz, dlaczego liczby nazywane są „skalarami”, ponieważ „skalują” wektor w górę lub w dół.)
Mnożenie wektora przez wektor (iloczyn kropkowy i iloczyn krzyżowy)
 |
Jak pomnożyć razem dwa wektory? Jest więcej niż jeden sposób!
(Przeczytaj te strony po więcej szczegółów.) |
Więcej niż 2 wymiary
Wektory działają również doskonale w 3 lub więcej wymiarach:
Wektor (1, 4, 5)
Przykład: dodaj wektory a = (3, 7, 4) i b = (2, 9, 11)
c = a + b
c = (3, 7, 4) + (2, 9, 11) = (3+2, 7+9, 4+11) = (5, 16, 15)
Przykład: jaka jest wielkość wektora w = (1, -2, 3) ?
|w| = √( 12 + (-2)2 + 32 ) = √( 1+4+9) = √14
Jest też przykład z 4 wymiarami (ale trudno go narysować!):
Przykład: odjąć (1, 2, 3, 4) od (3, 3, 3, 3)
(3, 3, 3, 3) + -(1, 2, 3, 4)
= (3, 3, 3, 3) + (-1,-2,-3,-4)
= (3-1, 3-2, 3-3, 3-4)
= (2, 1, 0, -1)
Wielkość i kierunek
Możemy znać wielkość i kierunek wektora, ale chcemy znać jego długości x i y (lub odwrotnie):
 |
<> |  |
| Wektor a we współrzędnych biegunowych | Wektor a w Cartesian Coordinates |
Możesz przeczytać jak je przekonwertować na Polar and Cartesian Coordinates, ale tutaj jest szybkie podsumowanie:
| Z współrzędnych biegunowych (r,θ) do współrzędnych kartezjańskich (x,y) |
Z współrzędnych kartezjańskich (x,y) do współrzędnych biegunowych (r,θ) |
|
|---|---|---|
|
|
Przykład
Sam i Alex ciągną skrzynię.
- Sam ciągnie z siłą 200 niutonów pod kątem 60°
- Aleks ciągnie z siłą 120 niutonów pod kątem 45°, jak pokazano na rysunku
Jaka jest łączna siła i jej kierunek?
Dodajmy te dwa wektory od głowy do ogona:
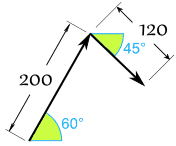
Najpierw przekonwertujmy z biegunowego na kartezjański (do 2 miejsc po przecinku):
Wektor Sama:
- x = r × cos( θ ) = 200 × cos(60°) = 200 × 0.5 = 100
- y = r × sin( θ ) = 200 × sin(60°) = 200 × 0.8660 = 173.21
Wektor Alexa:
- x = r × cos( θ ) = 120 × cos(-45°) = 120 × 0,7071 = 84,85
- y = r × sin( θ ) = 120 × sin(-45°) = 120 × -0.7071 = -84.85
Teraz mamy:
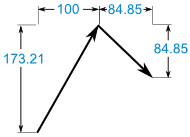
Dodaj je:
(100, 173.21) + (84.85, -84.85) = (184.85, 88.36)
Ta odpowiedź jest poprawna, ale przekonwertujmy ją z powrotem na biegunową, ponieważ pytanie było w biegunowej:
- r = √ ( x2 + y2 ) = √ ( 184.852 + 88.362 ) = 204.88
- θ = tan-1 ( y / x ) = tan-1 ( 88,36 / 184,85 ) = 25.5°
I mamy ten (zaokrąglony) wynik: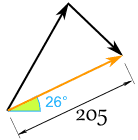
I wygląda to tak dla Sama i Alexa:
Mogliby uzyskać lepszy wynik, gdyby byli ramię w ramię!





