Ich werde häufig nach den wichtigsten Mathe-Formeln gefragt, die Schüler für den SAT wirklich wissen müssen. Nach 15 Jahren Nachhilfe in SAT-Mathematik habe ich eine kleine Liste mit den wichtigsten Formeln erstellt, die sich die Schüler merken sollten. Alles, was Sie zu diesem Thema wissen müssen, steht unten.

Wichtiger Hinweis: Die Formeln in diesem Beitrag sind für den alten SAT. Wenn Sie den SAT ab März 2016 ablegen werden, sollten Sie dem folgenden Link folgen: Math Formels for the Revised SAT

Quick Formula Reference Sheet

Ich habe auch ein schnelles Formel-Referenzblatt erstellt, das alle diese Formeln auflistet. Bitte lesen Sie diesen Beitrag mindestens einmal komplett durch, bevor Sie das Schnellreferenzblatt verwenden. Aber bewahren Sie dieses Blatt als schnelle Erinnerung auf, wenn Sie eine der Formeln vergessen haben. Drücken Sie den Button unten, um dieses PDF herunterzuladen.

SAT Mathe-Formeln

(1) Beginnen wir mit den Formeln, die Ihnen zu Beginn jedes SAT-Mathe-Teils gegeben werden. Prägen Sie sich diese ein. Hier sind sie.

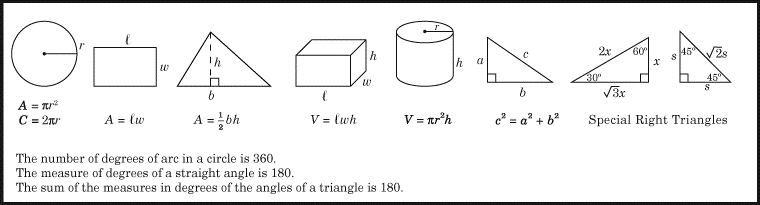
(2) Die folgende einfache Formel wird es Ihnen sehr leicht machen, Aufgaben zu lösen, bei denen es um prozentuale Veränderung geht.

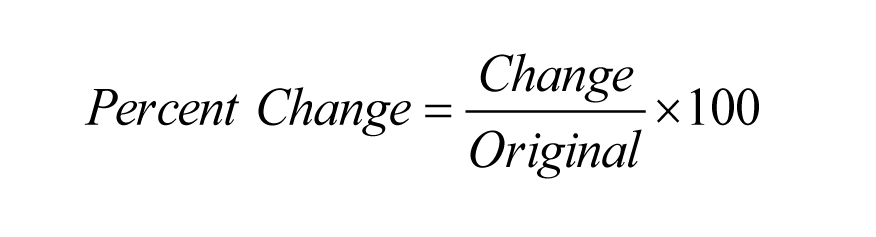
Beachten Sie, dass diese Formel sowohl für Probleme mit prozentualer Zunahme als auch für Probleme mit prozentualer Abnahme funktioniert.

Schauen wir uns ein einfaches Beispiel an:

Angenommen, x steigt von 8 auf 9. Um wie viel Prozent erhöht sich x?

Nun, der ursprüngliche Wert ist 8, und die Änderung ist 9 – 8 = 1. Daher haben wir

Prozentuale Änderung = 1/8 × 100 = 12,5.

So erhöht sich x um 12,5 %.

(3) Um einen Durchschnitt in eine Summe umzuwandeln, verwenden Sie die folgende Formel.

Summe = Durchschnitt – Anzahl

Mit dieser Formel lässt sich bei Statistikfragen aller Schwierigkeitsgrade oft viel Zeit sparen.

Schauen wir uns ein einfaches Beispiel an.

Der Durchschnitt (arithmetisches Mittel) von fünf Zahlen ist 20. Wenn eine sechste Zahl hinzugefügt wird, ist der Durchschnitt der sechs Zahlen 30. Wie lautet die sechste Zahl?

Nun, die Summe der fünf Zahlen ist 20 – 5 = 100.

Die Summe der sechs Zahlen ist 30 – 6 = 180.

Die sechste Zahl ist 180 – 100 = 80.

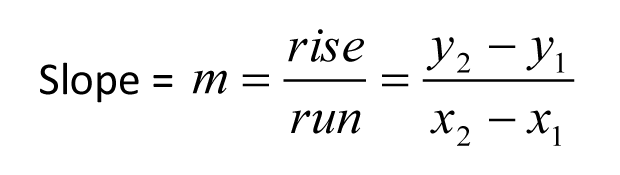
Hier sind (x1,y1) und (x2,y2) zwei beliebige Punkte auf der Geraden, und m steht für die Steigung. Beachten Sie, dass im Zähler zuerst die y-Koordinaten subtrahiert werden. Ein häufiger Fehler ist, die x-Koordinaten zuerst zu subtrahieren. Hier ist ein Beispiel.

Wie lautet die Steigung der Geraden, die durch die beiden Punkte (-1,3) und (2,5) verläuft?

Algebraische Lösung: Wir haben

y2 – y1 = 5 – 3 = 2, und x2 – x1 = 2 – (-1) = 2 + 1 = 3. Also m = 2/3.

Geometrische Lösung: Um von (-1, 3) nach (2,5) zu kommen, gehen wir 2 nach oben und 3 nach rechts. Also Anstieg = 2, und Lauf = 3. Daher ist m = 2/3.

Bemerkung: Um die geometrische Lösung besser zu verstehen, kann es hilfreich sein, die beiden Punkte zu zeichnen und visuell zu beobachten, wie man sich erst nach oben und dann nach rechts bewegen würde, um vom ersten zum zweiten Punkt zu gelangen.

(5) Zusätzlich zur Steigungsformel sollten Sie die Steigungs-Absatzform einer Geradengleichung kennen.

y = mx + b

Hier ist, wie üblich, m die Steigung der Geraden und b die y-Koordinate des y-Achsenabschnitts der Geraden.

Mit anderen Worten: Der Punkt (0,b) liegt auf der Geraden. b ist der Punkt, an dem die Gerade auf die y-Achse trifft.

Schreiben wir als Beispiel die Gleichung der Geraden, die eine Steigung von 3 hat und durch den Punkt (0,-5) geht.

Gegeben ist m = 3 und b = -5. Die Geradengleichung in Form des Steigungsabschnitts lautet also

y = 3x – 5.

Als Spezialfall der Gleichung y = mx + b ist zu beachten, dass eine waagerechte Gerade eine Gleichung der Form

y = b

Das liegt daran, dass die Steigung einer waagerechten Gerade 0 ist.

Zum Beispiel hat die horizontale Linie, die durch den Punkt (5, 3) verläuft, die Gleichung y = 3.

Sie sollten auch wissen, dass eine vertikale Linie eine Gleichung der Form

x = a

Beachten Sie, dass eine vertikale Linie keine Steigung hat und daher nicht in Steigungs-Absatz-Form geschrieben werden kann.

Zum Beispiel hat die vertikale Linie, die durch den Punkt (5, 3) verläuft, die Gleichung x = 5.

Sie sollten auch die folgenden beiden Fakten kennen:

Parallele Linien haben die gleiche Steigung.

Senkrechte Linien haben Steigungen, die negative Kehrwerte voneinander sind.

(6) Die Dreiecksregel besagt, dass

die dritte Seite eines Dreiecks zwischen der Differenz und der Summe der beiden anderen Seiten liegt.

Dies ist eine sehr einfache Regel, die im Unterricht oft nicht vermittelt wird. Probleme mit der Dreiecksregel neigen dazu, der Stufe 4 oder 5 zuzugehören, obwohl sie normalerweise recht einfach sind. Ich führe das auf die Tatsache zurück, dass viele Schüler diese Regel einfach nie gelernt haben. Hier ist ein einfaches Beispiel.

Wenn x eine ganze Zahl ist, wie viele verschiedene Dreiecke gibt es dann mit den Seitenlängen 2, 6 und x?

6 – 2 = 4, und 6 + 2 = 8. Nach der Dreiecksregel ist 4 < x < 8. Da x eine ganze Zahl sein muss, kann x 5, 6 oder 7 sein. Die Antwort ist also Drei.

(7) Diese nächste Formel ist manchmal nützlich, wenn man mit Mengen arbeitet. Wenn Sie eine Menge mit X Objekten und eine andere Menge mit Y Objekten haben, dann ist die Gesamtzahl der Objekte

Gesamt = X + Y – Beide + Keines

Schauen wir uns ein einfaches Beispiel an.

Es gibt 30 Schüler in einer Musikklasse. Von diesen Schülern spielen 10 Klavier, 15 spielen Gitarre und 3 spielen sowohl Klavier als auch Gitarre. Wie viele Schüler in der Klasse spielen keines dieser beiden Instrumente?

Setzt man diese Zahlen in die Formel ein, erhält man

30 = 10 + 15 – 3 + N.

So, N = 30 – 22 = 8.

(8) Viele Schüler kommen durcheinander, wenn sie die Anzahl der aufeinanderfolgenden ganzen Zahlen in einer Liste zählen.

Die Anzahl der ganzen Zahlen von a bis b, einschließlich, ist b – a + 1.

Merke: Das Wort „inklusive“ bedeutet, dass wir die Endpunkte a und b einschließen.

Zum Beispiel ist die Anzahl der ganzen Zahlen von 2 bis 7 gleich 7 – 2 + 1 = 6.

Das lässt sich leicht mit der Liste 2, 3, 4, 5, 6, 7 verifizieren.

Hier ist ein Beispiel, das schwieriger zu verifizieren ist.

Die Anzahl der ganzen Zahlen von 62 bis 512 ist 512 – 62 + 1 = 451.

(9) Eine letzte Formel, die jeder Schüler kennen sollte.

Entfernung = Geschwindigkeit – Zeit

Als einfaches Beispiel: Wenn Sie mit Ihrem Auto 5 Stunden lang mit einer Geschwindigkeit von 30 Meilen pro Stunde fahren, dann legen Sie (30)(5) = 150 Meilen zurück.

Für viele Studenten sollte das ausreichend sein. Wenn Sie derzeit in SAT Mathe unter 500 Punkten liegen, dann hören Sie bitte hier auf. Es gibt keinen Grund, sich mit diesen letzten paar Formeln zu verzetteln.

Für diejenigen unter Ihnen, die wirklich eine 800er Punktzahl erreichen wollen, sollten wir uns noch ein paar weitere ansehen.

(10) Zusätzlich zu der einfachen Formel Entfernung = Rate – Zeit, sollten sich fortgeschrittene Schüler die Formel für das harmonische Mittel merken.

Diese Formel kann verwendet werden, um die Durchschnittsgeschwindigkeit zu finden, wenn 2 individuelle Geschwindigkeiten für die gleiche Strecke bekannt sind. Hier ist ein Beispiel.

Dr. Steve fuhr mit einer Durchschnittsgeschwindigkeit von 40 Meilen pro Stunde zur Arbeit und mit einer Durchschnittsgeschwindigkeit von 60 Meilen pro Stunde von der Arbeit nach Hause. Wie hoch war seine Durchschnittsgeschwindigkeit für die gesamte Hin- und Rückfahrt in Meilen pro Stunde?

Wir setzen die angegebenen Zahlen einfach in die Formel für den harmonischen Mittelwert ein.

Wichtiger Hinweis: Ihre Intuition sagt Ihnen vielleicht, dass die Antwort auf diese Frage 50 Meilen pro Stunde sein sollte. In diesem Fall müssen wir jedoch den harmonischen Mittelwert und nicht den arithmetischen Mittelwert berechnen.

(11) Der fortgeschrittene Schüler möchte vielleicht auch den verallgemeinerten Satz des Pythagoras kennen.

d2 = a2 + b2 + c2

Diese einfache Formel wird verwendet, um die Länge der langen Diagonale eines rechteckigen Körpers zu finden. Hier ist ein einfaches Beispiel.

Wenn ein Kasten eine Länge von 3 Fuß, eine Breite von 4 Fuß und eine Höhe von 12 Fuß hat, was ist die längste Entfernung von einer Ecke des Kastens zu einer anderen Ecke des Kastens?

Die Frage fragt nach der Länge der langen Diagonale des Kastens. Wir setzen die Zahlen einfach in die Formel für den verallgemeinerten Satz des Pythagoras ein.

d2 = 32 + 42 + 122 = 169. Also d = 13.

(12) Die allgemeine Form für eine quadratische Funktion ist

y = ax2 + bx + c.

Der Graph dieser Funktion ist eine Parabel, deren Scheitelpunkt die x-Koordinate

Die Parabel öffnet sich nach oben, wenn a > 0 ist und nach unten, wenn a < 0 ist.

Hier ist ein Beispiel.

Lassen Sie die Funktion f durch f(x) = -2×2 – 3x + 2 definiert sein. Für welchen Wert von x hat die Funktion f ihren Maximalwert?

Der Graph dieser Funktion ist eine nach unten gerichtete Parabel, und wir sehen, dass a = -2 und b = -3. Die x-Koordinate des Scheitelpunkts ist also x = 3/(-4) = -3/4.

(13) Die Standardform für eine quadratische Funktion ist

y – k = a(x – h)2

Der Graph ist eine Parabel mit Scheitelpunkt bei (h,k). Auch hier öffnet sich die Parabel nach oben, wenn a > 0 und nach unten, wenn a < 0.

Hier ist ein Beispiel.

Lassen Sie die Funktion f durch f(x) = 3(x – 1)2 + 2 definiert sein. Für welchen Wert von x hat die Funktion f ihren Minimalwert?

Der Graph dieser Funktion ist eine nach oben gerichtete Parabel mit Scheitelpunkt (1,2). Daher ist die Antwort 1.

Bemerken: Beachten Sie, dass in diesem Beispiel k = 2 ist und auf der rechten Seite der Gleichung steht, statt auf der linken.

(14) Die Gesamtzahl der Grade im Inneren eines n-seitigen Polygons ist

(n – 2) – 180

Zum Beispiel, ein achtseitiges Polygon (oder Achteck) hat

(8 – 2) – 180 = 6 – 180 = 1080 Grad

in seinem Inneren. Daher hat jeder Winkel eines regelmäßigen Achtecks

1080/8 = 135 Grad.

Merke: Ein regelmäßiges Vieleck ist ein Vieleck, bei dem alle Seiten gleich lang und alle Winkel gleich groß sind.

Es gibt nicht viele Formeln, die Sie sich für SAT Mathe merken müssen, und viele davon kennen Sie wahrscheinlich schon. Machen Sie es sich also zur Aufgabe, die restlichen Formeln, die in den Mathe-Teilen des SAT getestet werden, in den nächsten Tagen auswendig zu lernen. Dann können Sie sich auf das Üben der SAT-Matheaufgaben konzentrieren.

Schnellreferenzblatt für Formeln

Und vergessen Sie nicht, das Schnellreferenzblatt für Formeln herunterzuladen. Bewahren Sie dieses Blatt zur schnellen Erinnerung auf, wenn Sie eine der Formeln vergessen haben. Klicken Sie auf die Schaltfläche unten, um dieses PDF herunterzuladen.

Klicken Sie auf Play im Video unten, um alle Mathe-Formeln zu lernen, die Sie für den SAT auswendig lernen sollten

Viel Glück,

Dr. Steve
Get 800

p.s.: Vergessen Sie nicht, einen Blick auf das folgende Sonderangebot auf alle meine SAT-Mathe-Vorbereitungsbücher zu werfen: SAT Math Prep Books Full Bundle