Ik krijg vaak vragen over de belangrijkste wiskundige formules die studenten echt moeten kennen voor de SAT. Na 15 jaar bijles te hebben gegeven in SAT wiskunde, heb ik een kleine lijst gemaakt van de belangrijkste formules die studenten moeten onthouden. Alles wat je moet weten over dit onderwerp staat hieronder.

Belangrijke opmerking: De formules in deze post zijn voor de oude SAT. Als je de SAT vanaf maart 2016 gaat doen, kun je het beste de volgende link volgen: Math Formulas for the Revised SAT

Quick Formula Reference Sheet

Ik heb ook een quick formula reference sheet gemaakt waarin al deze formules staan. Lees deze hele post ten minste een keer door voordat je de quick reference sheet gebruikt. Maar houd dit blad in de buurt voor een snelle herinnering wanneer u een van de formules vergeet. Druk op de knop hieronder om deze PDF te downloaden.

SAT wiskundeformules

(1) Laten we beginnen met de formules die je aan het begin van elk SAT-wiskundeonderdeel te horen krijgt. Leer deze uit je hoofd. Hier zijn ze.

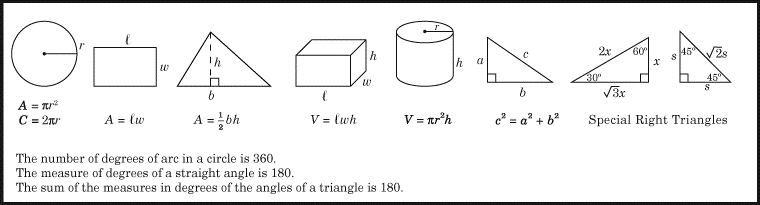
(2) Met de volgende eenvoudige formule kun je heel gemakkelijk problemen oplossen waarbij procentuele verandering een rol speelt.

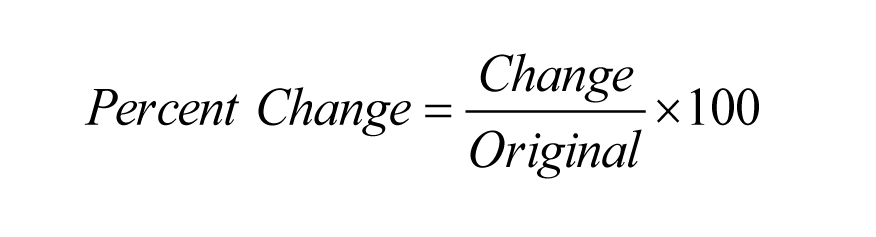
Merk op dat deze formule zowel werkt voor problemen met procentuele toename als voor problemen met procentuele afname.

Laten we eens kijken naar een eenvoudig voorbeeld:

Voorstel dat x toeneemt van 8 naar 9. Met hoeveel procent neemt x toe?

Wel, de oorspronkelijke waarde is 8, en de verandering is 9 – 8 = 1. Daarom hebben we

Percentage verandering = 1/8 × 100 = 12,5.

Dus x neemt toe met 12,5%.

(3) Om een gemiddelde te veranderen in een som, gebruik je de volgende formule.

Som = Gemiddelde – Aantal

Deze formule kan vaak worden gebruikt om veel tijd te besparen op statistiekvragen van alle moeilijkheidsgraden.

Laten we eens kijken naar een eenvoudig voorbeeld.

Het gemiddelde (rekenkundig gemiddelde) van vijf getallen is 20. Als een zesde getal wordt toegevoegd, is het gemiddelde van de zes getallen 30. Wat is het zesde getal?

Wel, de som van de vijf getallen is 20 – 5 = 100.

De som van de zes getallen is 30 – 6 = 180.

Het zesde getal is 180 – 100 = 80.

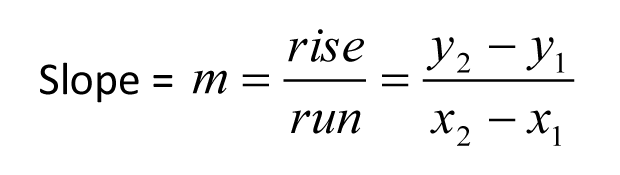
Hier zijn (x1,y1) en (x2,y2) willekeurige twee punten op de lijn, en m staat voor helling. Merk op dat de y-coördinaten eerst afgetrokken worden in de teller. Een veel voorkomende fout is om eerst de x-coördinaten af te trekken. Hier volgt een voorbeeld.

Wat is de richtingscoëfficiënt van de lijn die door de twee punten (-1,3) en (2,5) gaat?

Algebraïsche oplossing: We hebben

y2 – y1 = 5 – 3 = 2, en x2 – x1 = 2 – (-1) = 2 + 1 = 3. Dus m = 2/3.

Geometrische oplossing: Om van (-1, 3) naar (2,5) te komen gaan we 2 omhoog, en 3 naar rechts. Dus stijgen = 2, en lopen = 3. Daarom is m = 2/3.

Opmerking: Om de meetkundige oplossing beter te begrijpen kan het nuttig zijn om de twee punten te plotten, en visueel te observeren hoe je eerst omhoog, dan naar rechts zou bewegen om van het eerste punt naar het tweede punt te komen.

(5) Naast de hellingsformule moet je ook de hellingshoek-afsnijvorm van een vergelijking van een lijn kennen.

y = mx + b

Hier is, zoals gebruikelijk, m de helling van de lijn, en b de y-coördinaat van het y-afsnijpunt van de lijn.

Met andere woorden, het punt (0,b) ligt op de lijn. b is het punt waar de lijn de y-as raakt.

Als voorbeeld schrijven we een vergelijking van de lijn die een helling van 3 heeft en door het punt (0,-5) gaat.

We hebben gegeven dat m = 3, en b = -5. De vergelijking van de rechte in hellingshoek-afsnijvorm is dus

y = 3x – 5.

Als speciaal geval van de vergelijking y = mx + b geldt dat een horizontale lijn een vergelijking heeft van de vorm

y = b

Dit komt omdat de richtingscoëfficiënt van een horizontale lijn 0 is.

Bijv. de horizontale lijn door het punt (5, 3) heeft vergelijking y = 3.

Je moet ook weten dat een verticale lijn een vergelijking heeft van de vorm

x = a

Merk op dat een verticale lijn geen helling heeft, en dus niet in de vorm van een hellend intercept kan worden geschreven.

Bijv. de verticale lijn door het punt (5, 3) heeft vergelijking x = 5.

Je moet ook de volgende twee feiten weten:

Parallelle lijnen hebben dezelfde helling.

Perloodrechte lijnen hebben hellingen die negatieve reciproke van elkaar zijn.

(6) De driehoeksregel stelt dat

de derde zijde van een driehoek ligt tussen het verschil en de som van de andere twee zijden.

Dit is een heel eenvoudige regel die vaak niet wordt onderwezen in de klas. Opgaven met een driehoeksregel zijn meestal van niveau 4 of 5, ook al zijn ze meestal vrij gemakkelijk. Ik wijt dit aan het feit dat veel leerlingen deze regel gewoon nooit hebben geleerd. Hier is een eenvoudig voorbeeld.

Als x een geheel getal is, hoeveel verschillende driehoeken zijn er dan met zijden van lengte 2, 6 en x?

6 – 2 = 4, en 6 + 2 = 8. Door de driehoeksregel is 4 < x < 8. Omdat x een geheel getal moet zijn, kan x 5, 6, of 7 zijn. Het antwoord is dus Drie.

(7) Deze volgende formule komt soms van pas bij het omgaan met verzamelingen. Als je een verzameling hebt met X objecten en een andere verzameling met Y objecten, dan is het totaal aantal objecten

Totaal = X + Y – Beide + Geen van beide

Laten we eens kijken naar een eenvoudig voorbeeld.

Er zitten 30 leerlingen in een muziekklas. Van deze leerlingen spelen er 10 piano, 15 gitaar en 3 zowel piano als gitaar. Hoeveel leerlingen in de klas bespelen geen van beide instrumenten?

Substitueren we deze getallen in de formule, dan krijgen we

30 = 10 + 15 – 3 + N.

Dus, N = 30 – 22 = 8.

(8) Veel leerlingen raken in de war bij het tellen van het aantal opeenvolgende gehele getallen in een lijst.

Het aantal gehele getallen van a tot en met b is b – a + 1.

Merk op: Het woord “inclusief” betekent dat we de eindpunten a en b meerekenen.

Het aantal gehele getallen van 2 tot en met 7 is bijvoorbeeld 7 – 2 + 1 = 6.

Dit kan eenvoudig worden geverifieerd met de lijst 2, 3, 4, 5, 6, 7.

Hier volgt een voorbeeld dat moeilijker te verifiëren zou zijn.

Het aantal gehele getallen van 62 tot 512 is 512 – 62 + 1 = 451 .

(9) Nog een laatste formule die elke leerling moet kennen.

afstand = snelheid – tijd

Een eenvoudig voorbeeld: als je 5 uur lang met je auto 30 mijl per uur rijdt, dan leg je (30)(5) = 150 mijl af.

Voor veel studenten zou dat voldoende moeten zijn. Sterker nog, als je op dit moment minder dan 500 scoort voor wiskunde, stop hier dan alsjeblieft. Het is niet nodig om jezelf te verzwaren met deze laatste paar formules.

Voor degenen onder jullie die echt een 800 willen scoren, laten we er nog een paar bekijken.

(10) Naast de eenvoudige formule afstand = snelheid – tijd, zou de meer gevorderde student misschien de Harmonisch Gemiddelde Formule uit het hoofd willen leren.

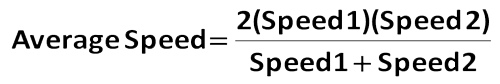
Deze formule kan worden gebruikt om de gemiddelde snelheid te vinden wanneer 2 individuele snelheden voor dezelfde afstand bekend zijn. Hier is een voorbeeld.

Dr. Steve reed naar zijn werk met een gemiddelde snelheid van 40 mijl per uur, en van zijn werk naar huis met een gemiddelde snelheid van 60 mijl per uur. Wat was zijn gemiddelde snelheid voor de hele heen- en terugreis, in mijl per uur?

We voeren de gegeven getallen gewoon in de Harmonische Gemiddelde Formule in.

Belangrijke opmerking: Je intuïtie zegt je misschien dat het antwoord op deze vraag 50 mijl per uur zou moeten zijn. In dit geval moeten we echter het harmonisch gemiddelde berekenen, en niet het rekenkundig gemiddelde.

(11) De gevorderde student wil misschien ook de Veralgemeende Stelling van Pythagoras kennen.

d2 = a2 + b2 + c2

Deze eenvoudige formule wordt gebruikt om de lengte van de lange diagonaal van een rechthoekig geheel te vinden. Hier volgt een eenvoudig voorbeeld.

Als een doos 3 voet lang, 4 voet breed en 12 voet hoog is, wat is dan de langste afstand van een hoek van de doos naar een andere hoek van de doos?

De vraag is om de lengte van de lange diagonaal van de doos te bepalen. We stoppen de getallen gewoon in de formule van de Algemene Stelling van Pythagoras.

d2 = 32 + 42 + 122 = 169. Dus d = 13.

(12) De algemene vorm voor een kwadratische functie is

y = ax2 + bx + c.

De grafiek van deze functie is een parabool waarvan het hoekpunt x-coördinaat

De parabool opent zich naar boven als a > 0 en naar beneden als a < 0.

Hier volgt een voorbeeld.

Laat de functie f gedefinieerd zijn door f(x) = -2×2 – 3x + 2. Voor welke waarde van x zal de functie f zijn maximum hebben?

De grafiek van deze functie is een neerwaartse parabool, en we zien dat a = -2, en b = -3. Dus de x-coördinaat van het hoekpunt is x = 3/(-4) = -3/4.

(13) De standaardvorm voor een kwadratische functie is

y – k = a(x – h)2

De grafiek is een parabool met hoekpunt op (h,k). Ook hier opent de parabool naar boven als a > 0 en naar beneden als a < 0.

Hier volgt een voorbeeld.

Laat de functie f gedefinieerd zijn door f(x) = 3(x – 1)2 + 2. Voor welke waarde van x zal de functie f zijn minimumwaarde hebben?

De grafiek van deze functie is een opwaarts gerichte parabool met hoekpunt (1,2). Het antwoord is dus 1.

Merk op: Merk op dat in dit voorbeeld k = 2, en het staat aan de rechterkant van de vergelijking in plaats van aan de linkerkant.

(14) Het totaal aantal graden in het binnenste van een veelhoek met n zijden is

(n – 2) – 180

Bijv, een achthoek heeft

(8 – 2) – 180 = 6 – 180 = 1080 graden

in zijn binnenste. Elke hoek van een regelmatige achthoek heeft dus

1080/8 = 135 graden.

Merk op: Een regelmatige veelhoek is een veelhoek waarvan alle zijden even lang zijn, en alle hoeken even groot.

Er zijn niet zo veel formules om uit je hoofd te leren voor SAT wiskunde, en veel van die formules ken je waarschijnlijk al. Dus maak er een punt van om de rest van deze formules, die getest worden op de wiskunde secties van de SAT, de komende dagen in je geheugen op te slaan. Dan kun je je concentreren op het oefenen van SAT wiskundeproblemen.

Quick Formula Reference Sheet

En vergeet niet om het quick formula reference sheet te downloaden. Houd dit blad bij de hand voor een snelle herinnering als je een van de formules bent vergeten. Druk op de knop hieronder om deze PDF te downloaden.

Klik op Afspelen in de video hieronder om alle wiskundige formules te leren die je moet onthouden voor de SAT