On me demande souvent quelles sont les formules mathématiques clés que les élèves doivent vraiment connaître pour le SAT. Après 15 ans de tutorat en mathématiques pour le SAT, j’ai créé une petite liste des formules les plus importantes que les élèves doivent mémoriser. Tout ce que vous devez savoir à ce sujet se trouve ci-dessous.

Note importante : les formules présentées dans ce billet concernent l’ancien SAT. Si vous devez passer le SAT à partir de mars 2016, vous pouvez suivre le lien suivant : Math Formulas for the Revised SAT

Quick Formula Reference Sheet

J’ai également créé une fiche de référence rapide des formules qui répertorie toutes ces formules. Veuillez lire l’intégralité de ce post au moins une fois avant d’utiliser la feuille de référence rapide. Mais gardez cette feuille à portée de main pour un rappel rapide lorsque vous oubliez l’une des formules. Appuyez sur le bouton ci-dessous pour télécharger ce PDF.

Formules mathématiques du SAT

(1) Commençons par les formules qui vous sont données au début de chaque section mathématique du SAT. Apprenez-les par cœur. Les voici.

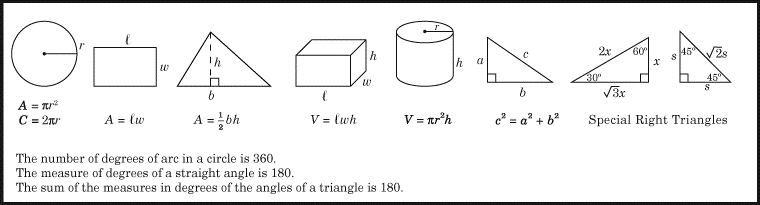
(2) La formule simple suivante vous permettra de résoudre très facilement les problèmes impliquant le pourcentage de changement.

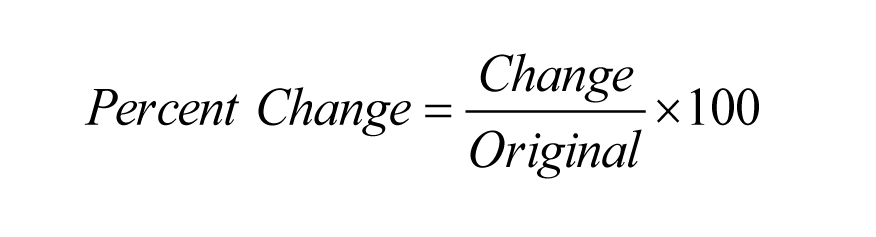
Notez que cette formule fonctionne aussi bien pour les problèmes impliquant une augmentation en pourcentage que pour les problèmes impliquant une diminution en pourcentage.

Regardons un exemple simple :

Supposons que x augmente de 8 à 9. De quel pourcentage x augmente-t-il ?

Eh bien, la valeur d’origine est 8, et le changement est 9 – 8 = 1. Par conséquent, nous avons

Le pourcentage de changement = 1/8 × 100 = 12,5.

Donc x augmente de 12,5 %.

(3) Pour changer une moyenne en somme, utilisez la formule suivante .

Somme = Moyenne – Nombre

Cette formule peut souvent être utilisée pour gagner beaucoup de temps sur des questions de statistiques de tous niveaux de difficulté.

Voyons un exemple simple.

La moyenne (moyenne arithmétique) de cinq nombres est 20. Lorsqu’on ajoute un sixième nombre, la moyenne des six nombres est de 30. Quel est le sixième nombre ?

Eh bien, la somme des cinq nombres est 20 – 5 = 100.

La somme des six nombres est 30 – 6 = 180.

Le sixième nombre est 180 – 100 = 80.

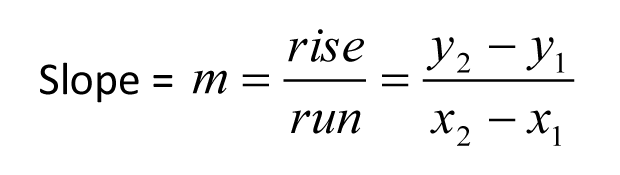
Ici, (x1,y1) et (x2,y2) sont deux points quelconques de la droite, et m représente la pente. Notez que les coordonnées y sont soustraites en premier dans le numérateur. Une erreur courante consiste à soustraire les coordonnées x en premier. Voici un exemple.

Quelle est la pente de la droite qui passe par les deux points (-1,3) et (2,5)?

Solution algébrique : On a

y2 – y1 = 5 – 3 = 2, et x2 – x1 = 2 – (-1) = 2 + 1 = 3. Donc m = 2/3.

Solution géométrique : Pour passer de (-1, 3) à (2,5), on monte de 2, et on monte de 3 à droite. Donc, montée = 2, et course = 3. Par conséquent, m = 2/3.

Remarque : Pour mieux comprendre la solution géométrique, il peut être utile de tracer les deux points et d’observer visuellement comment vous vous déplaceriez vers le haut, puis vers la droite pour aller du premier point au deuxième point.

(5) En plus de la formule de la pente, vous devriez connaître la forme de l’ordonnée à l’origine d’une équation d’une droite.

y = mx + b

Ici, comme d’habitude, m est la pente de la droite, et b est la coordonnée y de l’ordonnée à l’origine de la droite.

En d’autres termes, le point (0,b) est sur la droite. b est l’endroit où la droite touche l’axe des y.

À titre d’exemple, écrivons l’équation de la droite qui a une pente de 3 et passe par le point (0,-5).

On nous donne m = 3, et b = -5. Ainsi, l’équation de la droite sous la forme de l’ordonnée à l’origine de la pente est

y = 3x – 5.

Comme cas particulier de l’équation y = mx + b, notons qu’une droite horizontale a une équation de la forme

y = b

C’est parce que la pente d’une droite horizontale est 0.

Par exemple, la droite horizontale passant par le point (5, 3) a pour équation y = 3.

Vous devez également savoir qu’une droite verticale a une équation de la forme

x = a

Notez qu’une droite verticale n’a pas de pente, et ne peut donc pas être écrite sous la forme de l’ordonnée à l’origine.

Par exemple, la droite verticale passant par le point (5, 3) a pour équation x = 5.

Vous devez également connaître les deux faits suivants :

Les lignes parallèles ont la même pente.

Les lignes perpendiculaires ont des pentes qui sont les réciproques négatives les unes des autres.

(6) La règle du triangle stipule que

le troisième côté d’un triangle est compris entre la différence et la somme des deux autres côtés.

C’est une règle très simple qui n’est souvent pas enseignée en classe. Les problèmes de la règle du triangle ont tendance à être de niveau 4 ou 5 même s’ils sont généralement assez faciles. J’attribue cela au fait que de nombreux étudiants n’ont tout simplement jamais appris cette règle. Voici un exemple simple.

Si x est un nombre entier, combien de triangles différents y a-t-il avec des côtés de longueur 2, 6 et x ?

6 – 2 = 4, et 6 + 2 = 8. Par la règle du triangle, 4 < x < 8. Puisque x doit être un nombre entier, x peut être 5, 6 ou 7. La réponse est donc Trois.

(7) Cette prochaine formule s’avère parfois utile lorsqu’on traite des ensembles. Si vous avez un ensemble avec X objets et un autre ensemble avec Y objets, alors le nombre total d’objets est

Total = X + Y – Les deux + Ni l’un ni l’autre

Regardons un exemple simple.

Il y a 30 élèves dans un cours de musique. Parmi ces élèves, 10 jouent du piano, 15 jouent de la guitare, et 3 jouent à la fois du piano et de la guitare. Combien d’élèves de la classe ne jouent d’aucun de ces deux instruments ?

Substituant ces nombres dans la formule, on a

30 = 10 + 15 – 3 + N.

Donc, N = 30 – 22 = 8.

(8) De nombreux élèves s’embrouillent lorsqu’il s’agit de compter le nombre d’entiers consécutifs dans une liste.

Le nombre d’entiers de a à b inclus est b – a + 1.

Remarque : Le mot « inclusif » signifie que l’on inclut les extrémités a et b.

Par exemple, le nombre d’entiers de 2 à 7 est 7 – 2 + 1 = 6.

Cela peut être facilement vérifié avec la liste 2, 3, 4, 5, 6, 7.

Voici un exemple qui serait plus difficile à vérifier.

Le nombre d’entiers de 62 à 512 est 512 – 62 + 1 = 451 .

(9) Une dernière formule que tout élève devrait connaître .

distance = vitesse – temps

A titre d’exemple simple, si vous conduisez votre voiture à une vitesse de 30 miles par heure pendant 5 heures, alors vous parcourrez (30)(5) = 150 miles.

Pour de nombreux étudiants, cela devrait être suffisant. En fait, si vous obtenez actuellement un score inférieur à 500 en mathématiques au SAT, alors arrêtez-vous ici. Il n’est pas nécessaire de vous enliser avec ces quelques dernières formules.

Pour ceux d’entre vous qui veulent vraiment obtenir un score de 800, examinons-en quelques autres.

(10) En plus de la formule simple distance = taux – temps, l’étudiant plus avancé pourrait vouloir mémoriser la formule de moyenne harmonique.

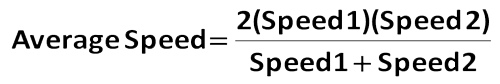
Cette formule peut être utilisée pour trouver la vitesse moyenne lorsque 2 vitesses individuelles pour la même distance sont connues. Voici un exemple.

Le docteur Steve se rendait au travail à une vitesse moyenne de 40 miles par heure, et rentrait du travail à une vitesse moyenne de 60 miles par heure. Quelle était sa vitesse moyenne pour l’ensemble du trajet aller-retour, en miles par heure ?

Il nous suffit de brancher les nombres donnés dans la formule de moyenne harmonique.

Note importante : votre intuition pourrait vous dire que la réponse à cette question devrait être 50 miles par heure. Dans ce cas, cependant, nous devons calculer la moyenne harmonique, et non la moyenne arithmétique.

(11) L’étudiant avancé peut également vouloir connaître le théorème de Pythagore généralisé.

d2 = a2 + b2 + c2

Cette formule simple permet de trouver la longueur de la grande diagonale d’un solide rectangulaire. Voici un exemple simple.

Si une boîte a une longueur de 3 pieds, une largeur de 4 pieds et une hauteur de 12 pieds, quelle est la plus longue distance d’un coin de la boîte à un autre coin de la boîte ?

La question demande la longueur de la longue diagonale de la boîte. Il suffit de brancher les chiffres dans la formule du théorème de Pythagore généralisé.

d2 = 32 + 42 + 122 = 169. Donc d = 13.

(12) La forme générale d’une fonction quadratique est

y = ax2 + bx + c.

Le graphe de cette fonction est une parabole dont le sommet a pour coordonnée x-.coordonnée

La parabole s’ouvre vers le haut si a > 0 et vers le bas si a < 0.

Voici un exemple.

Définissons la fonction f par f(x) = -2×2 – 3x + 2. Pour quelle valeur de x la fonction f aura-t-elle sa valeur maximale ?

Le graphique de cette fonction est une parabole orientée vers le bas, et on voit que a = -2, et b = -3. Donc la coordonnée x du sommet est x = 3/(-4) = -3/4.

(13) La forme standard d’une fonction quadratique est

y – k = a(x – h)2

Le graphique est une parabole dont le sommet est à (h,k). Là encore, la parabole s’ouvre vers le haut si a > 0 et vers le bas si a < 0.

Voici un exemple.

Définissons la fonction f par f(x) = 3(x – 1)2 + 2. Pour quelle valeur de x la fonction f aura-t-elle sa valeur minimale ?

Le graphe de cette fonction est une parabole orientée vers le haut avec le sommet (1,2). Par conséquent, la réponse est 1.

Remarque : Notez que dans cet exemple k = 2, et qu’il est à droite de l’équation au lieu d’être à gauche.

(14) Le nombre total de degrés à l’intérieur d’un polygone à n côtés est

(n – 2) – 180

Par exemple, un polygone à huit côtés (ou octogone) a

(8 – 2) – 180 = 6 – 180 = 1080 degrés

dans son intérieur. Par conséquent, chaque angle d’un octogone régulier a

1080/8 = 135 degrés.

Remarque : Un polygone régulier est un polygone dont tous les côtés ont la même longueur, et tous les angles la même mesure.

Il n’y a pas tant de formules à mémoriser pour les mathématiques du SAT, et beaucoup d’entre elles, vous les connaissez probablement déjà. Faites donc en sorte de mémoriser le reste de ces formules, testées dans les sections mathématiques du SAT, au cours des prochains jours. Vous pourrez ensuite vous concentrer sur la pratique des problèmes de mathématiques du SAT.

Fiche de référence des formules rapides

Et n’oubliez pas de télécharger la fiche de référence des formules rapides. Gardez cette feuille à portée de main pour un rappel rapide lorsque vous oubliez l’une des formules. Appuyez sur le bouton ci-dessous pour télécharger ce PDF.

Cliquez sur Lecture dans la vidéo ci-dessous pour apprendre toutes les formules mathématiques que vous devez mémoriser pour le SAT