Fórmulas Matemáticas a Memorizar para o SAT Após 15 anos de aulas de matemática do SAT, criei uma pequena lista das fórmulas mais importantes que os alunos devem memorizar. Tudo o que precisa de saber sobre este assunto está abaixo.
Nota importante: As fórmulas neste post são para o SAT antigo. Se vai fazer o SAT a partir de Março de 2016, pode querer seguir o seguinte link: Fórmulas Matemáticas para o SAT Revisto
Folha de Referência de Fórmula Rápida
Criei também uma folha de referência de fórmula rápida que lista todas estas fórmulas. Por favor, leia todo este post pelo menos uma vez antes de utilizar a folha de referência rápida. Mas guarde esta folha para um lembrete rápido quando esquecer uma das fórmulas. Prima o botão abaixo para descarregar este PDF.
![]()
br>>
SAT Math Formulas
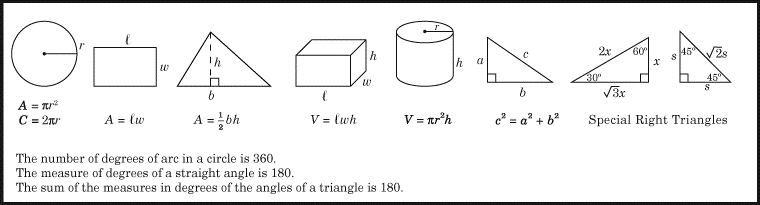
(1) Comecemos com as fórmulas que lhe são dadas no início de cada secção matemática do SAT. Memorize-as. Aqui estão.

(2) A seguinte fórmula simples facilitar-lhe-á muito a resolução de problemas que envolvam Mudança Percentual.
Nota que esta fórmula funciona tanto para problemas envolvendo aumento percentual como para problemas envolvendo diminuição percentual.
Vejamos um exemplo simples:
Ponhamos que x aumenta de 8 para 9. Em que percentagem é que x aumenta?
Bem, o valor Original é 8, e a Mudança é 9 – 8 = 1. Portanto, temos
Mudança percentual = 1/8 × 100 = 12,5,
Então x aumenta 12,5%,
(3) Para alterar uma média para uma soma, use a seguinte fórmula.
Soma = Média – Número
Esta fórmula pode ser frequentemente utilizada para poupar muito tempo em questões estatísticas de todos os níveis de dificuldade.
Vejamos um exemplo simples.
A média (média aritmética) de cinco números é 20. Quando um sexto número é adicionado, a média dos seis números é 30. Qual é o sexto número?
Bem, a soma dos cinco números é 20 – 5 = 100.
A soma dos seis números é 30 – 6 = 180.
O sexto número é 180 – 100 = 80.
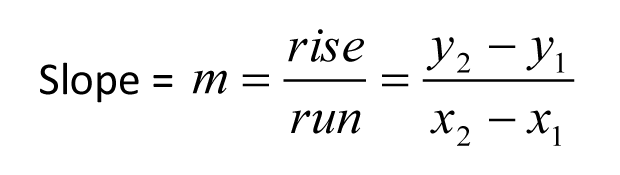
Aqui, (x1,y1) e (x2,y2) são quaisquer dois pontos na linha, e m representa a inclinação. Note-se que as coordenadas y são subtraídas em primeiro lugar no numerador. Um erro comum é subtrair primeiro as coordenadas-x. Eis um exemplo.
Qual é a inclinação da linha que passa pelos dois pontos (-1,3) e (2,5)?
Solução algébrica: Temos
y2 – y1 = 5 – 3 = 2, e x2 – x1 = 2 – (-1) = 2 + 1 = 3. Então m = 2/3.
Solução geométrica: Para passar de (-1, 3) a (2,5) subimos 2, e à direita 3. Então sobe = 2, e corre = 3. Portanto, m = 2/3.
Remark: Para compreender melhor a solução geométrica, pode ser útil traçar os dois pontos, e observar visualmente como se subiria, depois direito a passar do primeiro ponto para o segundo ponto.
(5) Para além da fórmula da inclinação, deve conhecer a forma de intercepção da inclinação de uma equação de uma linha.
y = mx + b
Aqui, como habitualmente, m é a inclinação da linha, e b é a coordenada y do intercepção y da linha.
Por outras palavras, o ponto (0,b) está na linha. b é onde a linha atinge o eixo y.
Como exemplo, vamos escrever uma equação da linha que tem uma inclinação de 3 e passa pelo ponto (0,-5).
Damos que m = 3, e b = -5. Assim, a equação da linha na forma inclinada é
y = 3x – 5.
Como um caso especial da equação y = mx + b, note-se que uma linha horizontal tem uma equação da forma
y = b
Isto porque a inclinação de uma linha horizontal é 0.
Por exemplo, a linha horizontal que passa pelo ponto (5, 3) tem a equação y = 3.
Também se deve saber que uma linha vertical tem uma equação da forma
x = a
Nota que uma linha vertical não tem inclinação, e portanto não pode ser escrita de forma inclinada.
Por exemplo, a linha vertical que passa pelo ponto (5, 3) tem a equação x = 5.
Também deve conhecer os dois factos seguintes:
Linhas paralelas têm a mesma inclinação.
Linhas perpendiculares têm declives que são recíprocos negativos uma da outra.
(6) A regra do triângulo declara que
o terceiro lado de um triângulo está entre a diferença e a soma dos outros dois lados.
Esta é uma regra muito simples que muitas vezes não é ensinada na sala de aula. Os problemas de regra triangular tendem a ser de nível 4 ou 5, embora sejam geralmente bastante fáceis. Atribuo isto ao facto de muitos estudantes simplesmente nunca terem aprendido esta regra. Eis um exemplo simples.
Se x é um número inteiro, quantos triângulos diferentes existem com lados de comprimento 2, 6 e x?
6 – 2 = 4, e 6 + 2 = 8. Pela regra do triângulo, 4 < x < 8. Como x deve ser um número inteiro, x pode ser 5, 6, ou 7. Portanto, a resposta é Three.
(7) Esta fórmula seguinte vem por vezes a calhar quando se lida com conjuntos. Se tiver um conjunto com X objectos e outro conjunto com Y objectos, então o número total de objectos é
Total = X + Y – Ambos + Nenhum
Vejamos um exemplo simples.
Há 30 alunos numa aula de música. Destes estudantes, 10 tocam piano, 15 tocam guitarra, e 3 tocam tanto piano como guitarra. Quantos alunos da turma não tocam nenhum destes dois instrumentos?
Substituindo estes números na fórmula, temos
30 = 10 + 15 – 3 + N.
Então, N = 30 – 22 = 8.
(8) Muitos estudantes ficam confusos ao contar o número de inteiros consecutivos numa lista.
O número de inteiros de a a a b, inclusive é b – a + 1.
Remarcar: A palavra “inclusive” significa que estamos a incluir os pontos finais a e b.
Por exemplo, o número de inteiros de 2 a 7 é 7 – 2 + 1 = 6.
Isso pode ser facilmente verificado com a lista 2, 3, 4, 5, 6, 7.
Aqui está um exemplo que seria mais difícil de verificar.
O número de inteiros de 62 a 512 é 512 – 62 + 1 = 451 .
(9) Uma última fórmula que todos os alunos devem conhecer.
distance = taxa – tempo
Como exemplo simples, se conduzir o seu carro a uma velocidade de 30 milhas por hora durante 5 horas, então irá viajar (30)(5) = 150 milhas.
Para muitos estudantes, isso deve ser suficiente. De facto, se está actualmente a pontuar abaixo de 500 em matemática SAT, então por favor pare aqui. Não há necessidade de se atolar com estas últimas fórmulas.
Para aqueles que realmente querem pontuar um 800, vejamos mais algumas.
(10) Para além da simples fórmula distância = taxa – tempo, o aluno mais avançado poderá querer memorizar a Fórmula da Média Harmónica.
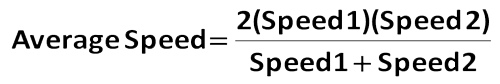
Esta fórmula pode ser utilizada para encontrar a velocidade média quando são conhecidas 2 velocidades individuais para a mesma distância. Aqui está um exemplo.
Dr. Steve conduziu para o trabalho a uma velocidade média de 40 milhas por hora, e para casa do trabalho a uma velocidade média de 60 milhas por hora. Qual foi a sua velocidade média durante toda a viagem de ida e volta, em milhas por hora?
Só ligamos os números dados à Fórmula da Média Harmónica.
Nota importante: A sua intuição pode dizer-lhe que a resposta a esta pergunta deve ser 50 milhas por hora. Neste caso, contudo, precisamos de calcular a Média Harmónica, e não a Média Aritmética.
(11) O estudante avançado pode também querer conhecer o Teorema de Pitágoras Generalizado.
d2 = a2 + b2 + c2
Esta fórmula simples é utilizada para encontrar o comprimento da diagonal longa de um sólido rectangular. Aqui está um exemplo simples.
Se uma caixa tem um comprimento de 3 pés, uma largura de 4 pés, e altura de 12 pés, qual é a maior distância de um canto da caixa para outro canto da caixa?
A questão é pedir o comprimento da diagonal longa da caixa. Basta ligar os números à fórmula do Teorema de Pitágoras Generalizado.
d2 = 32 + 42 + 122 = 169. So d = 13.
(12) A forma geral para uma função quadrática é
y = ax2 + bx + c.
O gráfico desta função é uma parábola cujo vértice tem x-coordinate
![]()
A parábola abre para cima se a > 0 e para baixo se a < 0.
Aqui está um exemplo.
Deixe a função f ser definida por f(x) = -2×2 – 3x + 2. Para que valor de x terá a função f o seu valor máximo?
O gráfico desta função é uma parábola virada para baixo, e vemos que a = -2, e b = -3. Assim, a coordenada x do vértice é x = 3/(-4) = -3/4.
(13) A forma padrão para uma função quadrática é
y – k = a(x – h)2
O gráfico é uma parábola com vértice em (h,k). Novamente, a parábola abre-se para cima se a > 0 e para baixo se a < 0.
Aqui está um exemplo.
Deixe a função f ser definida por f(x) = 3(x – 1)2 + 2. Para que valor de x terá a função f o seu valor mínimo?
O gráfico desta função é uma parábola virada para cima com vértice (1,2). Portanto, a resposta é 1.
Remark: Note-se que neste exemplo k = 2, e está no lado direito da equação em vez de estar no lado esquerdo.
(14) O número total de graus no interior de um polígono com n faces é
(n – 2) – 180
Por exemplo, um polígono de oito lados (ou octógono) tem
(8 – 2) – 180 = 6 – 180 = 1080 graus
no seu interior. Portanto, cada ângulo de um octógono regular tem
1080/8 = 135 graus.
Remark: Um polígono regular é um polígono com todos os lados iguais em comprimento, e todos os ângulos iguais em medida.
Não há muitas fórmulas a memorizar para SAT matemática, e muitas delas provavelmente já conhece. Portanto, faça questão de memorizar o resto destas fórmulas, testadas nas secções matemáticas do SAT, durante os próximos dias. Depois pode concentrar-se na prática dos problemas de matemática do SAT.
Folha de referência rápida da fórmula
E não se esqueça de descarregar a folha de referência rápida da fórmula. Guarde esta folha para um lembrete rápido quando esquecer uma das fórmulas. Prima o botão abaixo para descarregar este PDF.
![]()
Click Play in the Video Below to Learn All The Math Formulas You Should Memorize For The SAT
Best of luck,
Dr. Steve
Get 800
p.s.: Não se esqueça de ver a seguinte oferta especial em todos os meus livros de preparação matemática para o SAT: SAT Math Prep Books Full Bundle

