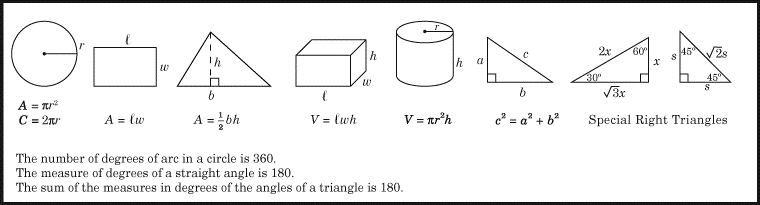
(2) La seguente semplice formula vi renderà molto facile risolvere i problemi che riguardano la variazione percentuale.

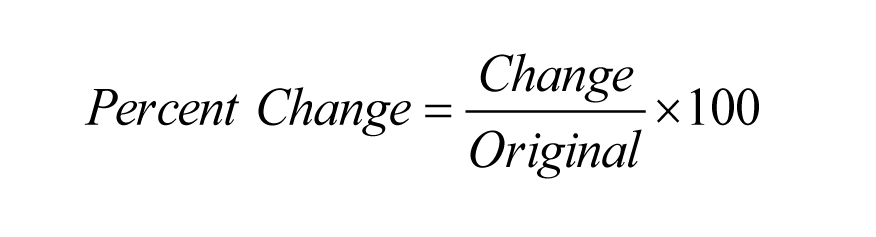
Nota che questa formula funziona sia per problemi che riguardano l’aumento percentuale sia per problemi che riguardano la diminuzione percentuale.

Guardiamo un semplice esempio:

Supponiamo che x aumenti da 8 a 9. Di quale percentuale aumenta x?

Bene, il valore originale è 8, e la variazione è 9 – 8 = 1. Perciò abbiamo

Cambio percentuale = 1/8 × 100 = 12.5.

Quindi x aumenta del 12.5%.

(3) Per cambiare una media in una somma, usa la seguente formula.

Somma = Media – Numero

Questa formula può essere spesso usata per risparmiare molto tempo nelle domande di statistica di tutti i livelli di difficoltà.

Vediamo un semplice esempio.

La media (media aritmetica) di cinque numeri è 20. Quando si aggiunge un sesto numero, la media dei sei numeri è 30. Qual è il sesto numero?

Ebbene, la somma dei cinque numeri è 20 – 5 = 100.

La somma dei sei numeri è 30 – 6 = 180.

Il sesto numero è 180 – 100 = 80.

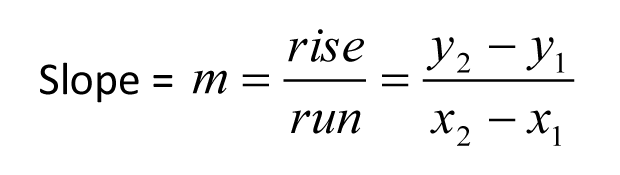
Qui, (x1,y1) e (x2,y2) sono due punti qualsiasi della retta, e m sta per pendenza. Si noti che le coordinate y sono sottratte per prime al numeratore. Un errore comune è quello di sottrarre prima le coordinate x. Ecco un esempio.

Qual è la pendenza della retta che passa per i due punti (-1,3) e (2,5)? Abbiamo

y2 – y1 = 5 – 3 = 2, e x2 – x1 = 2 – (-1) = 2 + 1 = 3. Quindi m = 2/3.

Soluzione geometrica: Per andare da (-1, 3) a (2,5) ci spostiamo su di 2, e a destra di 3. Quindi salire = 2, e correre = 3. Pertanto, m = 2/3.

Ricordo: Per comprendere meglio la soluzione geometrica può essere utile tracciare i due punti, e osservare visivamente come ci si muoverebbe verso l’alto e poi verso destra per andare dal primo al secondo punto.

(5) Oltre alla formula della pendenza, si dovrebbe conoscere la forma dell’intercetta della pendenza dell’equazione di una retta.

y = mx + b

Qui, come al solito, m è la pendenza della retta e b è l’ordinata dell’intercetta y della retta.

In altre parole, il punto (0,b) è sulla retta. b è il punto in cui la retta colpisce l’asse y.

Come esempio, scriviamo l’equazione della retta che ha una pendenza di 3 e passa per il punto (0,-5).

Ci è dato che m = 3, e b = -5. Quindi, l’equazione della retta in forma di intercetta di pendenza è

y = 3x – 5.

Come caso speciale dell’equazione y = mx + b, si noti che una retta orizzontale ha un’equazione della forma

y = b

Questo perché la pendenza di una retta orizzontale è 0.

Per esempio, la retta orizzontale che passa per il punto (5, 3) ha equazione y = 3.

Si dovrebbe anche sapere che una retta verticale ha un’equazione della forma

x = a

Si noti che una retta verticale non ha pendenza, e quindi non può essere scritta in forma di intercetta di pendenza.

Per esempio, la retta verticale che passa per il punto (5, 3) ha equazione x = 5.

Bisogna anche conoscere i due fatti seguenti:

Le rette parallele hanno la stessa pendenza.

Le rette perpendicolari hanno pendenze reciproche negative.

(6) La regola del triangolo afferma che

il terzo lato di un triangolo è compreso tra la differenza e la somma degli altri due lati.

Questa è una regola molto semplice che spesso non viene insegnata in classe. I problemi sulla regola del triangolo tendono ad essere di livello 4 o 5 anche se di solito sono abbastanza facili. Attribuisco questo al fatto che molti studenti semplicemente non hanno mai imparato questa regola. Ecco un semplice esempio.

Se x è un numero intero, quanti triangoli diversi ci sono con lati di lunghezza 2, 6 e x?

6 – 2 = 4, e 6 + 2 = 8. Per la regola del triangolo, 4 < x < 8. Poiché x deve essere un numero intero, x può essere 5, 6 o 7. Quindi la risposta è Tre.

(7) Questa prossima formula a volte è utile quando si tratta di insiemi. Se avete un insieme con X oggetti e un altro insieme con Y oggetti, allora il numero totale di oggetti è

Totale = X + Y – Entrambi + Nessuno dei due

Guardiamo un semplice esempio.

Ci sono 30 studenti in una classe di musica. Di questi studenti, 10 suonano il piano, 15 la chitarra e 3 suonano sia il piano che la chitarra. Quanti studenti della classe non suonano nessuno di questi due strumenti?

Sostituendo questi numeri nella formula, abbiamo

30 = 10 + 15 – 3 + N.

Quindi, N = 30 – 22 = 8.

(8) Molti studenti si confondono quando contano il numero di interi consecutivi in una lista.

Il numero di interi da a a b, incluso è b – a + 1.

Ricordo: La parola “incluso” significa che stiamo includendo i punti finali a e b.

Per esempio, il numero di interi da 2 a 7 è 7 – 2 + 1 = 6.

Questo può essere facilmente verificato con la lista 2, 3, 4, 5, 6, 7.

Ecco un esempio che sarebbe più difficile da verificare.

Il numero di interi da 62 a 512 è 512 – 62 + 1 = 451.

(9) Un’ultima formula che ogni studente dovrebbe conoscere.

distanza = velocità – tempo

Come semplice esempio, se si guida la macchina ad una velocità di 30 miglia all’ora per 5 ore, allora si percorrerà (30)(5) = 150 miglia.

Per molti studenti, questo dovrebbe essere sufficiente. Infatti, se attualmente hai un punteggio inferiore a 500 nel SAT matematico, allora per favore fermati qui. Non c’è bisogno di impantanarsi con queste ultime formule.

Per quelli di voi che vogliono davvero ottenere un punteggio di 800, vediamone altre.

(10) Oltre alla semplice formula distanza = velocità – tempo, lo studente più avanzato potrebbe voler memorizzare la formula della media armonica.

Questa formula può essere usata per trovare la velocità media quando sono note 2 velocità individuali per la stessa distanza. Ecco un esempio.

Il dottor Steve andava al lavoro a una velocità media di 40 miglia all’ora e tornava a casa dal lavoro a una velocità media di 60 miglia all’ora. Qual è stata la sua velocità media per l’intero viaggio di andata e ritorno, in miglia all’ora?

Dobbiamo semplicemente inserire i numeri dati nella formula della media armonica.

Nota importante: Il vostro intuito potrebbe dirvi che la risposta a questa domanda dovrebbe essere 50 miglia all’ora. In questo caso, però, dobbiamo calcolare la media armonica, e non la media aritmetica.

(11) Lo studente avanzato potrebbe anche voler conoscere il Teorema di Pitagora generalizzato.

d2 = a2 + b2 + c2

Questa semplice formula si usa per trovare la lunghezza della diagonale lunga di un solido rettangolare. Ecco un esempio semplice.

Se una scatola ha una lunghezza di 3 piedi, una larghezza di 4 piedi e un’altezza di 12 piedi, qual è la distanza più lunga da un angolo della scatola a un altro angolo della scatola?

La domanda chiede la lunghezza della diagonale lunga della scatola. Basta inserire i numeri nella formula del Teorema di Pitagora Generalizzato.

d2 = 32 + 42 + 122 = 169. Quindi d = 13.

(12) La forma generale di una funzione quadratica è

y = ax2 + bx + c.

Il grafico di questa funzione è una parabola il cui vertice ha x-coordinata

La parabola si apre verso l’alto se a > 0 e verso il basso se a < 0.

Ecco un esempio.

Lasciamo che la funzione f sia definita da f(x) = -2×2 – 3x + 2. Per quale valore di x la funzione f avrà il suo valore massimo?

Il grafico di questa funzione è una parabola rivolta verso il basso, e vediamo che a = -2, e b = -3. Quindi l’ascissa del vertice è x = 3/(-4) = -3/4.

(13) La forma standard per una funzione quadratica è

y – k = a(x – h)2

Il grafico è una parabola con vertice in (h,k). Di nuovo, la parabola si apre verso l’alto se a > 0 e verso il basso se a < 0.

Ecco un esempio.

Lasciamo che la funzione f sia definita da f(x) = 3(x – 1)2 + 2. Per quale valore di x la funzione f avrà il suo valore minimo?

Il grafico di questa funzione è una parabola ascendente con vertice (1,2). Pertanto, la risposta è 1.

Nota: Si noti che in questo esempio k = 2, ed è sul lato destro dell’equazione invece che su quello sinistro.

(14) Il numero totale di gradi all’interno di un poligono di n lati è

(n – 2) – 180

Per esempio, un poligono di otto lati (o ottagono) ha

(8 – 2) – 180 = 6 – 180 = 1080 gradi

al suo interno. Quindi ogni angolo di un ottagono regolare ha

1080/8 = 135 gradi.

Ricordo: Un poligono regolare è un poligono con tutti i lati di uguale lunghezza, e tutti gli angoli di uguale misura.

Non ci sono molte formule da memorizzare per la matematica del SAT, e molte di esse probabilmente le conoscete già. Quindi fai in modo di memorizzare il resto di queste formule, testate nelle sezioni di matematica del SAT, nei prossimi giorni. Poi potrai concentrarti sulla pratica dei problemi di matematica del SAT.

Foglio di riferimento delle formule rapide

E non dimenticare di scaricare il foglio di riferimento delle formule rapide. Tieni questo foglio in giro per un rapido promemoria quando dimentichi una delle formule. Premi il pulsante qui sotto per scaricare questo PDF.

Clicca Play nel video qui sotto per imparare tutte le formule matematiche che dovresti memorizzare per il SAT