私はよく、学生がSATで本当に知っておくべき重要な数学の公式について質問を受けます。 私は15年間、SATの数学を教えてきましたが、生徒が覚えるべき最も重要な公式の小さなリストを作成しました。
重要なお知らせ:この記事にある公式は旧SAT用です。 2016年3月からSATを受験する方は、以下のリンクを参考にしてください。 Math Formulas for the Revised SAT
Quick Formula Reference Sheet
また、これらの公式をすべてリストアップしたクイック・フォーミュラ・リファレンス・シートを作成しました。 クイックリファレンスシートを使用する前に、この記事全体を少なくとも一度は読んでください。 しかし、このシートを手元に置いておけば、公式の1つを忘れたときにすぐに思い出すことができます。
![]()
SAT Math Formulas
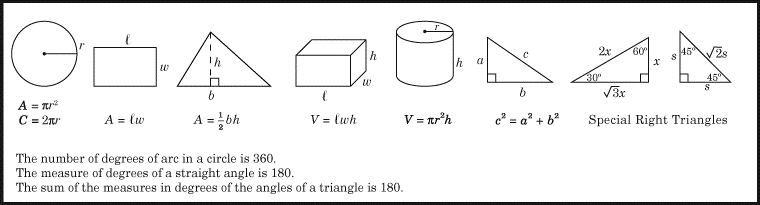
(1)まず、SATの各数学セクションの最初に与えられる公式から説明します。 これを暗記してください。

(2)次の簡単な公式を使えば、Percent Changeを含む問題をとても簡単に解くことができます。
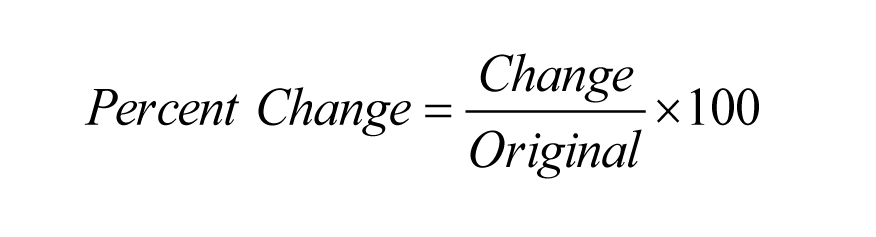
この公式は、パーセントの増加を伴う問題とパーセントの減少を伴う問題の両方に有効であることに注意してください。
簡単な例を見てみましょう。
さて、元の値は8、変化は9 – 8 = 1です。 したがって、
変化率=1/8×100=12.5.
だから、xは12.5%増加したことになります。
(3)平均値を和に変えるには、次の式を使います。
和=平均-数
この式を使うと、あらゆる難易度の統計問題で時間を大幅に短縮できることがよくあります。
簡単な例を見てみましょう。
5つの数字の平均(算術平均)は20です。 6個目の数字を加えると、6個の数字の平均は30になります。
さて、5つの数字の和は20 – 5 = 100、
6つの数字の和は30 – 6 = 180、
6つ目の数字は180 – 100 = 80となります。
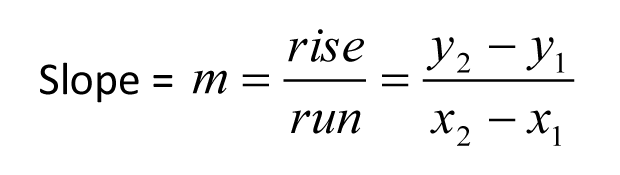
ここで、(x1,y1)と(x2,y2)は直線上の任意の2点で、mは傾きを表しています。 ここで、分子の中でy座標が最初に引かれていることに注意してください。 よくある間違いは、x座標を先に引いてしまうことです。
2点(-1,3)と(2,5)を通る直線の傾きは何ですか?
y2 – y1 = 5 – 3 = 2、x2 – x1 = 2 – (-1) = 2 + 1 = 3となり、m = 2/3となります。
幾何学的な解答です。 (-1, 3)から(2, 5)に行くには、上に2、右に3移動します。 つまり、上昇=2、走行=3となります。 したがって、m = 2/3となります。
備考。
備考:幾何学的解をよりよく理解するためには、2つの点をプロットして、最初の点から2番目の点に行くために、どのように上に、そして右に移動するかを視覚的に観察するとよいでしょう。
y = mx + b
ここで、いつものようにmは直線の傾き、bは直線のy切片のy座標です。
つまり、点(0,b)は直線上にあります。
例として、傾きが3で点(0,5)を通る直線の方程式を書いてみましょう
m=3、b=-5と与えられます。
方程式y = mx + bの特別な場合として、水平線の方程式が
y = b
水平線の傾きが0であることに注意してください。
例えば、点(5, 3)を通る水平線は、y = 3という方程式を持ちます。
また、垂直線は次のような式を持つことも知っておきましょう
x = a
なお、垂直線には傾きがないため、傾き-切片の形では書けません。
例えば、点(5, 3)を通る垂直線はx=5の方程式を持ちます。
また、次の2つの事実も知っておく必要があります:
平行線は同じ傾きを持ち、
垂直線の傾きはお互いに負の逆数である。
(6) 三角の法則とは、
三角形の3辺は、他の2辺の差と和の間にあるというものです。 三角形の法則の問題は、通常は非常に簡単であるにもかかわらず、レベル4または5になる傾向があります。 これは、多くの学生が単にこのルールを学んだことがないためだと考えています。
xを整数とすると、辺の長さが2、6、xの三角形は何種類ありますか。
< x < 8となります。 xは整数でなければならないので、xは5、6、7のいずれかになります。
(7) この次の式は、集合を扱うときに便利なことがあります。 X個の物体を持つ集合とY個の物体を持つ集合がある場合、物体の総数は
Total = X + Y – Both + Neither
簡単な例を見てみましょう。
音楽教室に30人の生徒がいます。 このうち、ピアノを弾く人が10人、ギターを弾く人が15人、ピアノとギターの両方を弾く人が3人います。
これらの数字を式に代入すると、
30 = 10 + 15 – 3 + Nとなります。
(8) リストの中の連続した整数の数を数えるとき、多くの学生が混乱します。
aからbまでの整数の数は、b – a + 1です。
注意してください。
例えば、2から7までの整数の個数は、7 – 2 + 1 = 6となります。
これは2、3、4、5、6、7というリストで簡単に検証できます。
検証が難しい例を挙げます。
62から512までの整数の数は、512 – 62 + 1 = 451 .
(9)最後に学生なら誰でも知っておくべき公式を一つ。
distance = rate – time
簡単な例として、時速30マイルのスピードで車を5時間走らせた場合、(30)(5)=150マイル移動することになります。
多くの学生にとっては、これで十分でしょう。 実際、もしあなたが現在SATの数学で500点以下のスコアを取っているのであれば、ここで止めてください。
本気で800点を取りたい人のために、もう少し見てみましょう。
(10) distance = rate – time という単純な式に加えて、上級者は Harmonic Mean Formula を覚えておくといいかもしれません。
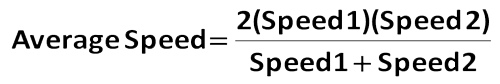
この式は、同じ距離の2つの速度が分かっている場合に、平均速度を求めるのに使用できます。
スティーブ博士は、平均時速40マイルで通勤し、平均時速60マイルで帰宅していました。
Dr.Steveは職場で平均時速40マイル、自宅で平均時速60マイルで運転していましたが、往復の平均速度は時速何マイルでしたか?
重要な注意点:この質問の答えは時速50マイルであるべきだと、直感的に思うかもしれません。
(11) 上級者は一般化されたピタゴラスの定理も知っておくとよいでしょう。
d2 = a2 + b2 + c2
この簡単な式は、直方体の長対角線の長さを求めるのに使われます。
ある箱の長さが3フィート、幅が4フィート、高さが12フィートの場合、その箱の一角から他の角までの最長距離は何ですか?
この質問は箱の長対角線の長さを求めています。
d2 = 32 + 42 + 122 = 169となります。
(12)二次関数の一般形は
y = ax2 + bx + cです。
この関数のグラフは、x-を頂点とする放物線である。座標
![]()
>< 0 であれば下向きに開きます。
以下に例を示します。
関数fをf(x)=-2×2 – 3x + 2で定義するとします。 この関数のグラフは下向きの放物線であり、a = -2、b = -3であることから、頂点のx座標はx = 3/(-4) = -3/4となります。
(13) 二次関数の標準形は
y – k = a(x – h)2
グラフは(h,k)を頂点とする放物線となります。 ここでも放物線は、< 0であれば下に開きます。
以下に例を示します。
関数fをf(x)=3(x – 1)2 + 2で定義するとします。 関数fはどのようなxの値で最小値をとるでしょうか。
この関数のグラフは頂点(1,2)を持つ上向きの放物線となります。 したがって、答えは1となります。
備考。 この例ではk=2であり、式の左端ではなく右端にあることに注意してください。
(14) n辺の多角形の内部の度数の合計は
(n – 2) – 180
例えば。 8辺の多角形(または八角形)は、その内部に
(8 – 2) – 180 = 6 – 180 = 1080度
の角度を持ちます。 したがって、正八角形の各角は
1080/8 = 135度
備考。
SATの数学で暗記すべき公式はそれほど多くなく、すでに知っているものも多いでしょう。 そのため、SATの数学セクションで出題されるこれらの公式の残りを数日間で記憶するようにしましょう。
Quick Formula Reference Sheet
また、Quick Formula Reference Sheetのダウンロードもお忘れなく。 このシートを手元に置いておけば、数式を忘れたときにすぐに思い出すことができます。 下のボタンを押して、このPDFをダウンロードしてください。
![]()
Click Play in the video Below to Learn All The Math Formulas You Should Memorize For The SAT
幸運をお祈りします。
Dr. Steve
Get 800
p.s: 私のSAT数学対策本全冊の以下のスペシャルオファーも忘れずにご覧ください。 SAT Math Prep Books Full Bundle


となります。