Teoria grafów >

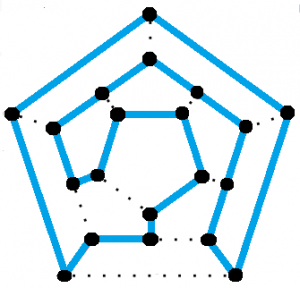
Dodecahedron (regularna figura bryłowa o dwunastu równych pięciokątnych ścianach) posiada cykl hamiltonowski.

Cykl hamiltonowski to zamknięta pętla w grafie, w której każdy węzeł (wierzchołek) jest odwiedzany dokładnie raz.

Pętla to krawędź, która łączy węzeł z samym sobą; więc cykl hamiltonowski to ścieżka podróżująca z punktu z powrotem do samego siebie, odwiedzając każdy węzeł po drodze.

Jeśli graf z więcej niż jednym węzłem (tj. graf niesingletonowy) ma tego typu cykl, nazywamy go grafem hamiltonowskim.

Nie ma żadnego równania ani ogólnej sztuczki, aby dowiedzieć się, czy graf ma cykl hamiltonowski; jedynym sposobem, aby to ustalić, jest wykonanie pełnego i wyczerpującego wyszukiwania, przechodząc przez wszystkie opcje.

Historia cyklu hamiltonowskiego

Nazwa cyklu pochodzi od Sir Williama Rowana Hamiltona, który w 1857 roku wymyślił grę logiczną polegającą na szukaniu cyklu hamiltonowskiego. Gra ta, zwana grą Icosian, została rozłożona jako graf dodekaedru z dziurą w każdym wierzchołku. Aby rozwiązać zagadkę lub wygrać grę, należało za pomocą kołków i sznurka znaleźć cykl Hamiltona – zamkniętą pętlę, która odwiedza każdy otwór dokładnie raz. Rozwiązanie pokazane jest na powyższym obrazku.

Przykłady grafów hamiltonowskich

Każdy graf pełny o więcej niż dwóch wierzchołkach jest grafem hamiltonowskim. Wynika to z definicji grafu pełnego: nieskierowany, prosty graf, w którym każda para węzłów jest połączona unikalną krawędzią.

Graf każdej bryły platońskiej jest grafem hamiltonowskim. Zatem graf sześcianu, czworościanu, ośmiościanu czy dwudziestościanu są grafami hamiltonowskimi z cyklami hamiltonowskimi.

Graf o n wierzchołkach (gdzie n > 3) jest hamiltonowski, jeśli suma stopni każdej pary niesąsiadujących wierzchołków jest n lub większa. Jest to znane jako twierdzenie Ore’a.

Zastosowania cykli hamiltonowskich i grafów

Poszukiwanie tych cykli nie jest tylko zabawą na wolne popołudnie. Ma ono realne zastosowania w tak różnych dziedzinach jak grafika komputerowa, projektowanie obwodów elektronicznych, mapowanie genomów i badania operacyjne.

Na przykład, podczas mapowania genomów naukowcy muszą połączyć wiele małych fragmentów kodu genetycznego („odczytów”, jak się je nazywa) w jedną sekwencję genomową („superstrunę”). Można tego dokonać poprzez znalezienie ścieżki lub cyklu Hamiltona, gdzie każdy z odczytów jest traktowany jako węzeł w grafie, a każde nałożenie (miejsce, gdzie koniec jednego odczytu pokrywa się z początkiem innego) jest traktowane jako krawędź.

W znacznie mniej złożonym zastosowaniu dokładnie tej samej matematyki, okręgi szkolne używają Hamiltonianów do planowania najlepszej trasy do odbierania uczniów z całego okręgu. Tutaj uczniowie mogą być uważani za węzły, ścieżki między nimi za krawędzie, a autobus chce jechać trasą, która minie dom każdego ucznia dokładnie raz.

Gra Icosian
On Hamiltonian Cycles and Hamiltonian Paths
Genome Assembly
Graph Algorithms in Bioinformatics

—————————————————————————–

Potrzebujesz pomocy w rozwiązaniu zadania domowego lub testu? W serwisie Chegg Study możesz uzyskać rozwiązanie swoich pytań krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!