Con frecuencia me preguntan sobre las fórmulas matemáticas clave que los estudiantes realmente necesitan saber para el SAT. Después de 15 años dando clases particulares de matemáticas para el SAT, he creado una pequeña lista de las fórmulas más importantes que los estudiantes deben memorizar. Todo lo que necesitas saber sobre este tema está abajo.
Nota importante: Las fórmulas de este post son para el antiguo SAT. Si vas a tomar el SAT a partir de marzo de 2016 es posible que quieras seguir el siguiente enlace: Math Formulas for the Revised SAT
Quick Formula Reference Sheet
También he creado una hoja de referencia de fórmulas rápidas que lista todas estas fórmulas. Por favor, lea todo este post al menos una vez antes de usar la hoja de referencia rápida. Pero mantén esta hoja cerca para un recordatorio rápido cuando olvides una de las fórmulas. Presione el botón de abajo para descargar este PDF.
![]()
Fórmulas de matemáticas del SAT
(1) Comencemos con las fórmulas que se le dan al principio de cada sección de matemáticas del SAT. Memorízalas. Aquí están.
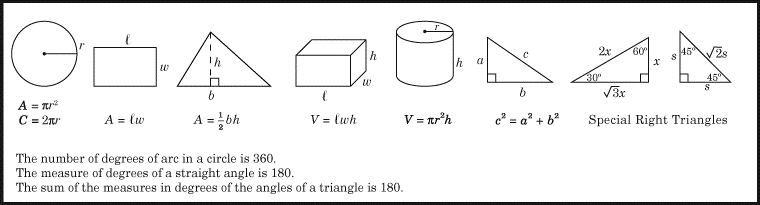

(2) La siguiente fórmula sencilla te facilitará mucho la resolución de problemas que impliquen Cambio porcentual.
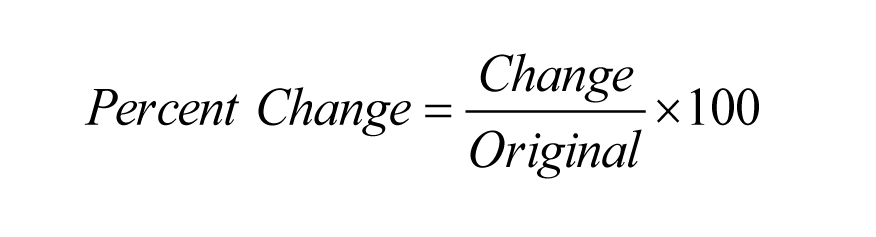
Nota que esta fórmula funciona tanto para problemas que implican un aumento porcentual como para problemas que implican una disminución porcentual.
Veamos un ejemplo sencillo:
Supongamos que x aumenta de 8 a 9. ¿En qué porcentaje aumenta x? En qué porcentaje aumenta x?
Bueno, el valor Original es 8, y el Cambio es 9 – 8 = 1. Por lo tanto, tenemos
Porcentaje de Cambio = 1/8 × 100 = 12,5.
Así que x aumenta un 12,5%.
(3) Para cambiar un promedio a una suma, utiliza la siguiente fórmula.
Suma = Media – Número
Esta fórmula se puede utilizar a menudo para ahorrar mucho tiempo en las preguntas de estadística de todos los niveles de dificultad.
Veamos un ejemplo sencillo.
La media (promedio aritmético) de cinco números es 20. Cuando se añade un sexto número, la media de los seis números es 30. Cuál es el sexto número?
Pues la suma de los cinco números es 20 – 5 = 100.
La suma de los seis números es 30 – 6 = 180.
El sexto número es 180 – 100 = 80.
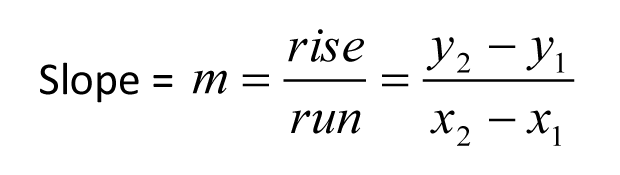
Aquí, (x1,y1) y (x2,y2) son dos puntos cualesquiera de la recta, y m representa la pendiente. Observa que las coordenadas y se restan primero en el numerador. Un error común es restar primero las coordenadas x. Aquí tienes un ejemplo.
¿Cuál es la pendiente de la recta que pasa por los dos puntos (-1,3) y (2,5)?
Solución algebraica: Tenemos
y2 – y1 = 5 – 3 = 2, y x2 – x1 = 2 – (-1) = 2 + 1 = 3. Por tanto, m = 2/3.
Solución geométrica: Para llegar de (-1, 3) a (2,5) nos movemos hacia arriba 2, y hacia la derecha 3. Por tanto, subida = 2, y carrera = 3. Por lo tanto, m = 2/3.
Atención: Para entender mejor la solución geométrica puede ser útil graficar los dos puntos, y observar visualmente cómo te moverías hacia arriba, y luego hacia la derecha para llegar del primer punto al segundo.
(5) Además de la fórmula de la pendiente, debes conocer la forma pendiente-intercepto de una ecuación de una recta.
y = mx + b
Aquí, como siempre, m es la pendiente de la recta, y b es la coordenada y de la intersección y de la recta.
En otras palabras, el punto (0,b) está en la recta. b es el punto en el que la recta choca con el eje y.
Como ejemplo, escribamos una ecuación de la recta que tiene una pendiente de 3 y pasa por el punto (0,-5).
Nos da que m = 3, y b = -5. Por tanto, la ecuación de la recta en forma pendiente-intercepto es
y = 3x – 5.
Como caso especial de la ecuación y = mx + b, observa que una recta horizontal tiene una ecuación de la forma
y = b
Esto es así porque la pendiente de una recta horizontal es 0.
Por ejemplo, la recta horizontal que pasa por el punto (5, 3) tiene ecuación y = 3.
También debes saber que una recta vertical tiene una ecuación de la forma
x = a
Nota que una recta vertical no tiene pendiente, y por tanto no puede escribirse en forma pendiente-intercepto.
Por ejemplo, la recta vertical que pasa por el punto (5, 3) tiene la ecuación x = 5.
También debes conocer los dos hechos siguientes:
Las rectas paralelas tienen la misma pendiente.
Las rectas perpendiculares tienen pendientes que son recíprocas negativas entre sí.
(6) La regla del triángulo establece que
el tercer lado de un triángulo está entre la diferencia y la suma de los otros dos lados.
Se trata de una regla muy sencilla que no suele enseñarse en el aula. Los problemas de la regla del triángulo suelen ser de nivel 4 o 5 aunque suelen ser bastante fáciles. Atribuyo esto al hecho de que muchos estudiantes simplemente nunca han aprendido esta regla. He aquí un ejemplo sencillo.
Si x es un número entero, ¿cuántos triángulos diferentes hay con lados de longitud 2, 6 y x?
6 – 2 = 4, y 6 + 2 = 8. Por la regla del triángulo, 4 < x < 8. Como x debe ser un número entero, x puede ser 5, 6 o 7. Así que la respuesta es Tres.
(7) Esta siguiente fórmula a veces es útil cuando se trata de conjuntos. Si tienes un conjunto con X objetos y otro conjunto con Y objetos, entonces el número total de objetos es
Total = X + Y – Ambos + Ninguno
Veamos un ejemplo sencillo.
Hay 30 alumnos en una clase de música. De estos alumnos, 10 tocan el piano, 15 tocan la guitarra y 3 tocan tanto el piano como la guitarra. ¿Cuántos alumnos de la clase no tocan ninguno de estos dos instrumentos?
Sustituyendo estos números en la fórmula, tenemos
30 = 10 + 15 – 3 + N.
Entonces, N = 30 – 22 = 8.
(8) Muchos alumnos se confunden al contar el número de enteros consecutivos de una lista.
El número de enteros de a a b, inclusive, es b – a + 1.
Recuerda: La palabra «inclusivo» significa que estamos incluyendo los puntos extremos a y b.
Por ejemplo, el número de enteros del 2 al 7 es 7 – 2 + 1 = 6.
Esto se puede comprobar fácilmente con la lista 2, 3, 4, 5, 6, 7.
Aquí tienes un ejemplo que sería más difícil de comprobar.
El número de enteros de 62 a 512 es 512 – 62 + 1 = 451 .
(9) Una última fórmula que todo estudiante debe conocer.
Distancia = tasa – tiempo
Como ejemplo sencillo, si conduces tu coche a una velocidad de 30 millas por hora durante 5 horas, entonces recorrerás (30)(5) = 150 millas.
Para muchos estudiantes, eso debería ser suficiente. De hecho, si actualmente tienes una puntuación inferior a 500 en matemáticas del SAT, entonces por favor detente aquí. No hay necesidad de atascarse con estas últimas fórmulas.
Para aquellos de ustedes que realmente quieren obtener una puntuación de 800, veamos algunas más.
(10) Además de la simple fórmula distancia = tasa – tiempo, el estudiante más avanzado podría querer memorizar la fórmula de la media armónica.
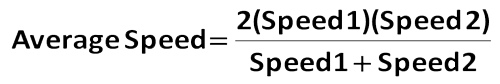
Esta fórmula se puede utilizar para encontrar la velocidad media cuando se conocen 2 velocidades individuales para la misma distancia. Aquí hay un ejemplo.
El Dr. Steve condujo al trabajo a una velocidad media de 40 millas por hora, y a casa desde el trabajo a una velocidad media de 60 millas por hora. ¿Cuál fue su velocidad media durante todo el viaje de ida y vuelta, en millas por hora?
Simplemente introducimos los números dados en la fórmula de la media armónica.
Nota importante: Tu intuición podría decirte que la respuesta a esta pregunta debería ser 50 millas por hora. En este caso, sin embargo, necesitamos calcular la Media Armónica, y no la Media Aritmética.
(11) El estudiante avanzado también puede querer conocer el Teorema de Pitágoras Generalizado.
d2 = a2 + b2 + c2
Esta sencilla fórmula se utiliza para encontrar la longitud de la diagonal larga de un sólido rectangular. He aquí un ejemplo sencillo.
Si una caja tiene una longitud de 3 pies, una anchura de 4 pies y una altura de 12 pies, ¿cuál es la distancia más larga de una esquina de la caja a otra esquina de la caja?
La pregunta pide la longitud de la diagonal larga de la caja. Sólo tenemos que introducir los números en la fórmula del Teorema de Pitágoras Generalizado.
d2 = 32 + 42 + 122 = 169. Así que d = 13.
(12) La forma general de una función cuadrática es
y = ax2 + bx + c.
La gráfica de esta función es una parábola cuyo vértice tiene x-coordenada
![]()
La parábola se abre hacia arriba si a > 0 y hacia abajo si a < 0.
Aquí tienes un ejemplo.
Deja que la función f esté definida por f(x) = -2×2 – 3x + 2. Para qué valor de x tendrá la función f su valor máximo?
La gráfica de esta función es una parábola orientada hacia abajo, y vemos que a = -2, y b = -3. Por tanto, la coordenada x del vértice es x = 3/(-4) = -3/4.
(13) La forma estándar de una función cuadrática es
y – k = a(x – h)2
La gráfica es una parábola con vértice en (h,k). De nuevo, la parábola se abre hacia arriba si a > 0 y hacia abajo si a < 0.
Aquí tienes un ejemplo.
Deja que la función f esté definida por f(x) = 3(x – 1)2 + 2. Para qué valor de x tendrá la función f su valor mínimo?
La gráfica de esta función es una parábola orientada hacia arriba con vértice (1,2). Por lo tanto, la respuesta es 1.
Recuerda: Observa que en este ejemplo k = 2, y está en el lado derecho de la ecuación en vez de en el izquierdo.
(14) El número total de grados en el interior de un polígono de n lados es
(n – 2) – 180
Por ejemplo, un polígono de ocho lados (u octógono) tiene
(8 – 2) – 180 = 6 – 180 = 1080 grados
en su interior. Por tanto, cada ángulo de un octógono regular tiene
1080/8 = 135 grados.
Recuerda: Un polígono regular es un polígono con todos los lados iguales en longitud, y todos los ángulos iguales en medida.
No hay tantas fórmulas que memorizar para las matemáticas del SAT, y muchas de ellas probablemente ya las conoces. Así que hazte el propósito de memorizar el resto de estas fórmulas, evaluadas en las secciones de matemáticas del SAT, en los próximos días. Luego puedes concentrarte en practicar los problemas de matemáticas del SAT.
Hoja de referencia de fórmulas rápidas
Y no olvides descargar la hoja de referencia de fórmulas rápidas. Ten esta hoja cerca para tener un recordatorio rápido cuando te olvides de una de las fórmulas. Pulsa el botón de abajo para descargar este PDF.
![]()
Haz clic en el play del vídeo de abajo para aprender todas las fórmulas matemáticas que debes memorizar para el SAT
Mucha suerte,
Dr. Steve
Consigue 800
p.s: No te olvides de echar un vistazo a la siguiente oferta especial en todos mis libros de preparación de matemáticas para el SAT: SAT Math Prep Books Full Bundle

