Często jestem pytany o kluczowe formuły matematyczne, które uczniowie naprawdę muszą znać dla SAT. Po 15 latach udzielania korepetycji z matematyki SAT, stworzyłem małą listę najważniejszych wzorów, które uczniowie powinni zapamiętać. Wszystko, co musisz wiedzieć na ten temat jest poniżej.

Ważna uwaga: Formuły w tym poście są dla starego SAT. Jeśli będziesz brać SAT zaczynając od marca 2016, możesz chcieć skorzystać z następującego linku: Math Formulas for the Revised SAT

Quick Formula Reference Sheet

Utworzyłem również szybki arkusz referencyjny formuły, który wymienia wszystkie te formuły. Proszę przeczytać cały ten post co najmniej raz przed użyciem szybkiego arkusza referencyjnego. Ale zachować ten arkusz wokół dla szybkiego przypomnienia, gdy zapomnisz jedną z formuł. Naciśnij poniższy przycisk, aby pobrać ten plik PDF.

SAT Matematyczne Formuły

(1) Zacznijmy od formuł, które są podane na początku każdej sekcji matematycznej SAT. Zapamiętaj je. Oto one.

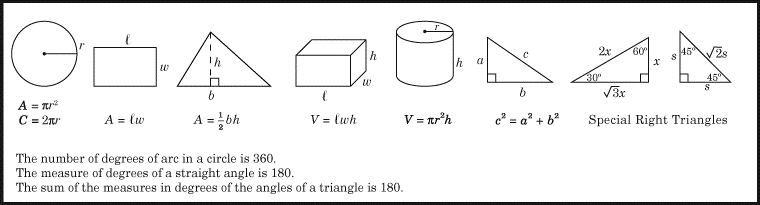
(2) Poniższa prosta formuła bardzo ułatwi Ci rozwiązywanie zadań dotyczących Zmiany procentowej.

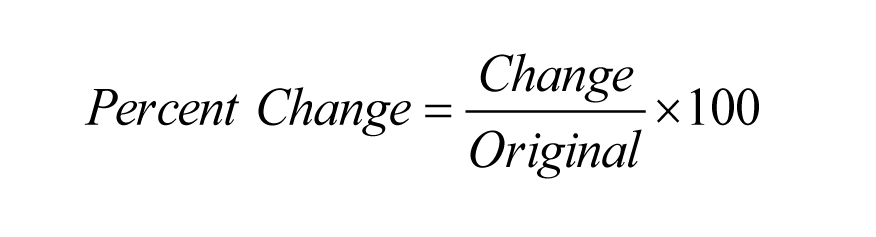
Zauważ, że ten wzór działa zarówno w przypadku problemów związanych z procentowym wzrostem, jak i problemów związanych z procentowym spadkiem.

Przyjrzyjrzyjmy się prostemu przykładowi:

Załóżmy, że x wzrasta z 8 do 9. O jaki procent wzrasta x?

Pierwotna wartość to 8, a Zmiana to 9 – 8 = 1. Mamy zatem

Zmiana procentowa = 1/8 × 100 = 12,5.

Więc x wzrasta o 12,5%.

(3) Aby zamienić średnią na sumę, użyj następującego wzoru.

Sum = Średnia – Liczba

Ta formuła może być często używana, aby zaoszczędzić dużo czasu na pytaniach dotyczących statystyki na wszystkich poziomach trudności.

Przyjrzyjrzyjmy się prostemu przykładowi.

Średnia (średnia arytmetyczna) pięciu liczb wynosi 20. Po dodaniu szóstej liczby, średnia z tych sześciu liczb wynosi 30. Jaka jest szósta liczba?

Cóż, suma pięciu liczb wynosi 20 – 5 = 100.

Suma sześciu liczb wynosi 30 – 6 = 180.

Szósta liczba wynosi 180 – 100 = 80.

Tutaj, (x1,y1) i (x2,y2) są dowolnymi dwoma punktami na prostej, a m oznacza nachylenie. Zauważ, że współrzędne y są odejmowane jako pierwsze w liczniku. Częstym błędem jest odejmowanie najpierw współrzędnych x. Oto przykład.

Jakie jest nachylenie prostej przechodzącej przez dwa punkty (-1,3) i (2,5)?

Rozwiązanie algebraiczne: Mamy

y2 – y1 = 5 – 3 = 2, oraz x2 – x1 = 2 – (-1) = 2 + 1 = 3. Zatem m = 2/3.

Rozwiązanie geometryczne: Aby dostać się z (-1, 3) do (2,5) przesuwamy się w górę o 2, a w prawo o 3. Zatem wzniesienie = 2, a bieg = 3. Stąd m = 2/3.

Rozwiązanie geometryczne: Aby lepiej zrozumieć rozwiązanie geometryczne, pomocne może być wykreślenie dwóch punktów i wizualna obserwacja, w jaki sposób poruszałbyś się w górę, a następnie w prawo, aby dostać się z pierwszego punktu do drugiego.

(5) Oprócz wzoru na nachylenie, powinieneś znać postać przechylenia równania prostej.

y = mx + b

Tutaj, jak zwykle, m jest nachyleniem prostej, a b jest współrzędną y punktu przecięcia prostej.

Innymi słowy, punkt (0,b) leży na prostej. b to miejsce, w którym prosta trafia na oś y.

Jako przykład napiszmy równanie prostej, która ma nachylenie 3 i przechodzi przez punkt (0,-5).

Dane jest nam, że m = 3, a b = -5. Zatem równanie tej prostej w postaci punktu przecięcia zboczy wynosi

y = 3x – 5.

Jako szczególny przypadek równania y = mx + b, zauważmy, że linia pozioma ma równanie postaci

y = b

To dlatego, że nachylenie linii poziomej wynosi 0.

Na przykład, prosta pozioma przechodząca przez punkt (5, 3) ma równanie y = 3.

Powinieneś również wiedzieć, że linia pionowa ma równanie postaci

x = a

Zauważ, że linia pionowa nie ma nachylenia, a zatem nie może być zapisana w postaci punktu przecięcia nachylenia.

Na przykład, prosta pionowa przechodząca przez punkt (5, 3) ma równanie x = 5.

Powinieneś również znać następujące dwa fakty:

Proste równoległe mają takie samo nachylenie.

Proste prostopadłe mają nachylenia, które są ujemnymi odwrotnościami siebie.

(6) Reguła trójkąta mówi, że

Trzeci bok trójkąta znajduje się pomiędzy różnicą i sumą dwóch pozostałych boków.

To bardzo prosta reguła, która często nie jest nauczana w klasie. Problemy z regułą trójkąta mają tendencję do bycia na poziomie 4 lub 5, mimo że zazwyczaj są dość łatwe. Przypisuję to faktowi, że wielu studentów po prostu nigdy nie nauczyło się tej reguły. Oto prosty przykład.

Jeśli x jest liczbą całkowitą, ile jest różnych trójkątów o bokach długości 2, 6 i x?

6 – 2 = 4, a 6 + 2 = 8. Z zasady trójkąta wynika, że 4 < x <8. Ponieważ x musi być liczbą całkowitą, x może być 5, 6 lub 7. Więc odpowiedź brzmi Trzy.

(7) Ta następna formuła czasami przydaje się, gdy mamy do czynienia z zestawami. Jeśli mamy zbiór z X obiektami i inny zbiór z Y obiektami, to całkowita liczba obiektów wynosi

Ogółem = X + Y – Oba + Żaden

Przyjrzyjrzyjmy się prostemu przykładowi.

W klasie muzycznej jest 30 uczniów. Spośród tych uczniów 10 gra na pianinie, 15 gra na gitarze, a 3 gra zarówno na pianinie, jak i na gitarze. Ilu uczniów w klasie nie gra na żadnym z tych dwóch instrumentów?

Wstawiając te liczby do wzoru, mamy

30 = 10 + 15 – 3 + N.

Więc, N = 30 – 22 = 8.

(8) Wielu uczniów myli się podczas liczenia liczby kolejnych liczb całkowitych na liście.

Liczba liczb całkowitych od a do b, włącznie wynosi b – a + 1.

Pamiętaj: Słowo „inclusive” oznacza, że uwzględniamy punkty końcowe a i b.

Na przykład, liczba liczb całkowitych od 2 do 7 wynosi 7 – 2 + 1 = 6.

Można to łatwo zweryfikować za pomocą listy 2, 3, 4, 5, 6, 7.

Jest przykład, który będzie trudniejszy do zweryfikowania.

Liczba liczb całkowitych od 62 do 512 wynosi 512 – 62 + 1 = 451 .

(9) Ostatni wzór, który każdy uczeń powinien znać.

Dystans = prędkość – czas

Jak prosty przykład, jeśli jedziesz samochodem z prędkością 30 mil na godzinę przez 5 godzin, to przejedziesz (30)(5) = 150 mil.

Dla wielu uczniów, to powinno wystarczyć. W rzeczywistości, jeśli jesteś obecnie scoring poniżej 500 w SAT matematyki, a następnie proszę zatrzymać się tutaj. Nie ma potrzeby, aby pogrążać się w tych kilku ostatnich formułach.

Dla tych z was, którzy naprawdę chcą zdobyć 800 punktów, spójrzmy na kilka innych.

(10) Oprócz prostego wzoru odległość = tempo – czas, bardziej zaawansowany uczeń może chcieć zapamiętać wzór na średnią harmoniczną.

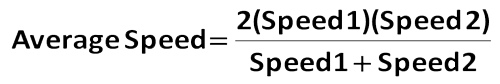
Wzór ten może być użyty do znalezienia średniej prędkości, gdy znane są 2 indywidualne prędkości dla tego samego dystansu. Oto przykład.

Dr Steve jechał do pracy ze średnią prędkością 40 mil na godzinę, a do domu z pracy ze średnią prędkością 60 mil na godzinę. Jaka była jego średnia prędkość dla całej podróży w obie strony, w milach na godzinę?

Po prostu wstawiamy podane liczby do wzoru na średnią harmoniczną.

Ważna uwaga: Twoja intuicja może Ci podpowiadać, że odpowiedzią na to pytanie powinno być 50 mil na godzinę. W tym przypadku jednak musimy obliczyć średnią harmoniczną, a nie średnią arytmetyczną.

(11) Zaawansowany student może również chcieć znać uogólnione twierdzenie pitagorejskie.

d2 = a2 + b2 + c2

Tego prostego wzoru używa się do znalezienia długości długiej przekątnej bryły prostokątnej. Oto prosty przykład.

Jeśli pudełko ma długość 3 stóp, szerokość 4 stóp i wysokość 12 stóp, jaka jest najdłuższa odległość od jednego rogu pudełka do innego rogu pudełka?

Pytanie dotyczy długości długiej przekątnej pudełka. Wystarczy podstawić te liczby do wzoru na uogólnione twierdzenie pitagorejskie.

D2 = 32 + 42 + 122 = 169. Zatem d = 13.

(12) Ogólna postać funkcji kwadratowej to

y = ax2 + bx + c.

Wykresem tej funkcji jest parabola, której wierzchołek ma współrzędne x-.współrzędną

Parabola otwiera się w górę, jeżeli a > 0 i w dół, jeżeli a < 0.

Podajemy przykład.

Pozwólmy, aby funkcja f była zdefiniowana przez f(x) = -2×2 – 3x + 2. Dla jakiej wartości x funkcja f będzie miała wartość maksymalną?

Wykresem tej funkcji jest parabola skierowana w dół, widzimy, że a = -2, a b = -3. Zatem współrzędna x wierzchołka to x = 3/(-4) = -3/4.

(13) Standardowa forma dla funkcji kwadratowej to

y – k = a(x – h)2

Wykresem jest parabola z wierzchołkiem w (h,k). Ponownie, parabola otwiera się w górę, jeśli a > 0 i w dół, jeśli a < 0.

Podajemy przykład.

Niech funkcja f będzie zdefiniowana przez f(x) = 3(x – 1)2 + 2. Dla jakiej wartości x funkcja f będzie miała wartość minimalną?

Wykresem tej funkcji jest parabola skierowana w górę o wierzchołku (1,2). Zatem odpowiedź brzmi 1.

Zaznacz: Zauważ, że w tym przykładzie k = 2, i jest po prawej stronie równania zamiast po lewej.

(14) Całkowita liczba stopni we wnętrzu n-bocznego wielokąta wynosi

(n – 2) – 180

Na przykład, ośmioboczny wielokąt (lub ośmiokąt) ma

(8 – 2) – 180 = 6 – 180 = 1080 stopni

w swoim wnętrzu. Zatem każdy kąt ośmiokąta foremnego ma

1080/8 = 135 stopni.

Pamiętaj: Wielokąt foremny to wielokąt, którego wszystkie boki mają równą długość, a wszystkie kąty równą miarę.

Nie ma tak wielu wzorów do zapamiętania na SAT matematyki, a wiele z nich prawdopodobnie już znasz. Więc zrobić to punkt popełnić resztę tych formuł, testowane na matematycznych sekcji SAT, do pamięci w ciągu najbliższych kilku dni. Wtedy będziesz mógł skupić się na ćwiczeniu zadań matematycznych SAT.

Szybki arkusz referencyjny formuł

Nie zapomnij też pobrać szybkiego arkusza referencyjnego formuł. Trzymaj ten arkusz w pobliżu dla szybkiego przypomnienia, gdy zapomnisz jednej z formuł. Naciśnij przycisk poniżej, aby pobrać ten plik PDF.

Kliknij Play in the Video Below to Learn All The Math Formulas You Should Memorize For The SAT

Powodzenia,

Dr. Steve
Get 800

p.s.: Nie zapomnij spojrzeć na następującą ofertę specjalną na wszystkich moich SAT matematyki prep książek: SAT Math Prep Books Full Bundle